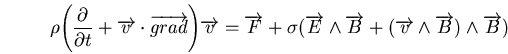C.4.14 Nombre de HARTMAN
Figure:
écoulement de HARTMAN
|
|
Pour traiter le problème illustré par la figure C.8,
réécrivons l'équation (C.12) sous la forme suivante :
Le terme
 représentant la somme de toutes les forces
non électromagnétiques. Dans l'approximation MHD
, on suppose que le
plasma est globalement neutre, donc
représentant la somme de toutes les forces
non électromagnétiques. Dans l'approximation MHD
, on suppose que le
plasma est globalement neutre, donc  .
De la même façon, réécrivons et simplifions l'équation (C.6) sous la forme
.
De la même façon, réécrivons et simplifions l'équation (C.6) sous la forme
Ceci permet alors d'écrire
D'après la section C.4.4, on a :
Donc l'équation de conservation de la quantité de mouvement s'écrit
Le terme
 décrit l'interaction entre un fluide se déplaçant à la vitesse
décrit l'interaction entre un fluide se déplaçant à la vitesse
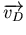 (vitesse de dérive cyclotron) et un fluide se déplaçant à la vitesse
(vitesse de dérive cyclotron) et un fluide se déplaçant à la vitesse
 . Un cas très proche a été traité en section
. Un cas très proche a été traité en section
![[*]](./icons/crossref.png) , sous la forme de deux strates de fluide à des vitesses différentes. Il s'agit donc d'une force de
viscosité magnétiqueC.33
de coefficient
, sous la forme de deux strates de fluide à des vitesses différentes. Il s'agit donc d'une force de
viscosité magnétiqueC.33
de coefficient  . Étant donné le coefficient de viscosité
dynamique d'un fluide, noté
. Étant donné le coefficient de viscosité
dynamique d'un fluide, noté  (par unité de surface), il est intéressant de comparer ces deux effets entre eux. Si
(par unité de surface), il est intéressant de comparer ces deux effets entre eux. Si  est une grandeur caractéristique du problème (donc
est une grandeur caractéristique du problème (donc  est une surface caractéristique), alors on définit le ratio entre
la viscosité magnétique et la viscosité du fluide par le nombre de
HartmanC.34 :
est une surface caractéristique), alors on définit le ratio entre
la viscosité magnétique et la viscosité du fluide par le nombre de
HartmanC.34 :
 |
(C.32) |
 étant la viscosité dynamique et
étant la viscosité dynamique et  le champ magnétique dans le plan perpendiculaire au mouvement.
En fonction du nombre de Hartman, l'écoulement aura un profil de vitesse bien particulier (voir figure
C.9 et figure C.10 les évaluations faites
avec une condition de vitesse nulle aux bords ; des champs électriques et
une hauteur normalisée). L'ouvrage [56] développe les caractéristiques de
ces courbes, ainsi que [71] qui introduit le nombre de Hartman dans
le contexte plus général des nombres sans dimension de l'hydrodynamique.
le champ magnétique dans le plan perpendiculaire au mouvement.
En fonction du nombre de Hartman, l'écoulement aura un profil de vitesse bien particulier (voir figure
C.9 et figure C.10 les évaluations faites
avec une condition de vitesse nulle aux bords ; des champs électriques et
une hauteur normalisée). L'ouvrage [56] développe les caractéristiques de
ces courbes, ainsi que [71] qui introduit le nombre de Hartman dans
le contexte plus général des nombres sans dimension de l'hydrodynamique.
Figure:
profil de vitesse d'un écoulement de HARTMAN
|
|
Figure:
profil de champ magnétique longitudinal d'un écoulement de
HARTMAN
|
|
Notes
- ...viscosité!magnétiqueC.33
- Il est possible aussi de considérer que les lignes de champ
magnétique perpendiculaires à la direction du mouvement sont partiellement gelées dans le plasma, donc le mouvement de ce
dernier est freiné par une force dissipative dépendant de la vitesse.
- ...
HartmanC.34
- Ce nombre est parfois appelé nombre de Chandrasekhar.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002