C.3.4 Conservation de la quantité de mouvement

D'après l'expression de la dérivée particulaire section C.1.2, et d'après les équations (C.11), (C.10) et (C.8), le principe fondamental de la dynamique s'écrit (par unité de volume) :

$$m \overrightarrow{\gamma} = \sum \overrightarrow{F_{ext\grave{e}rieures}}$$

$$\rho \Biggl( \frac{\partial}{\partial t} + \overrightarrow{v} \cdot \mathop{\overrightarrow{grad}} \Biggr) \overrightarrow{v} = - \mathop{\overrightarrow{grad}}({P}) + \rho \nu S \mathop{\nabla^2}(\overrightarrow{{v}}) + \rho_e \overrightarrow{E} \qquad$$

$$\qquad + \overrightarrow{j} \wedge \overrightarrow{B}$$ (C.12)

Il est également possible d'ajouter à cette équation une contribution dûe à la pression de radiation, via le terme 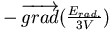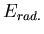$- \mathop{\overrightarrow{grad}}({\frac{E_{rad.}}{3 V}})$ ($E_{rad.}$ représentant l'énergie contenue dans le champ de radiation dans un volume $V$, et le fait de diviser cette densité d'énergie par trois pour obtenir une pression est une approximation courante).