C.4.4 Fréquence cyclotronique

Considérons une particule de charge $q$ soumise à la seule force de Lorentz (voir équation (C.8)). En projetant le principe fondamental de la dynamique sur le plan transverse au champ magnétique et en supposant que $E_{\perp} = 0$ (c'est à dire qu'il n'y a pas de champ électrique dans le plan perpendiculaire au champ magnétique^C.19), on fait apparaitre une équation caractéristique d'un mouvement circulaire et uniforme de fréquence de rotation :

$$\Omega_q = \frac{\mid \overrightarrow{v_{\perp}} \mid}{R} = \frac{\mid q \overrightarrow{B} \mid}{m}$$ (C.15)

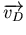Dans le cas d'un plasma suffisamment dilué, ou bien de champs suffisamment forts, la conductivité devient donc influencée par le champ magnétique. Supposons maintenant qu'il existe un champ électrique $\overrightarrow{E_{\perp}}$ (donc perpendiculaire à $\overrightarrow{B}$). Il suffit alors d'ajouter à $\overrightarrow{v_{\perp}}$ une vitesse $\overrightarrow{v_D}$ telle que $\overrightarrow{E_{\perp}} + \overrightarrow{v_D} \wedge \overrightarrow{B} = \overrightarrow{0}$ pour retrouver une configuration plus générale mais similaire à ce qui a été traité précédemment ; on appelle vitesse de dérive $\overrightarrow{v_D}=\frac{\overrightarrow{E_{\perp}} \wedge \overrightarrow{B}} {\overrightarrow{B}^2}$.

Notes

... magnétique^C.19

Dans le cas d'un champ électrique parallèle au champ magnétique, la particule est accélérée sous l'influence de $\overrightarrow{E}$ sans action de $\overrightarrow{B}$.