C.2 Équations de MAXWELL pour la MHD
On se place dans l'approximation d'un fluide continu, conducteur électrique, pour lequel le courant de déplacement est
négligeable (donc pas d'accumulation de charges électriques, c'est à dire dans l'hypothèse de la quasi-neutralité
électrique : ce qui se traduit par
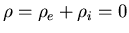 ).On a alors :
).On a alors :
Nous nous plaçons dans le cas d'un matériau quelconque où nous avons les
relationsC.3:
On écrira donc généralement ceci sous la forme :
Cet ensemble d'équations constitue les équations de MaxwellC.4. Fréquemment en MHD
, on néglige le courant de déplacement
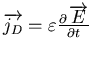 devant le
courant de conduction
devant le
courant de conduction
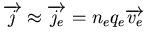 (voir
équation D.2 page
(voir
équation D.2 page ![[*]](./icons/crossref.png) avec
avec 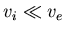 ).
).
Notes
- ...
relationsC.3
 étant la conductivité,
étant la conductivité,  étant la
permitivité magnétique et
étant la
permitivité magnétique et  étant la perméabilitémagnétique du matériau
étant la perméabilitémagnétique du matériau
- ... MaxwellC.4
- En combinant l'équation (C.1)
avec la divergence de l'équation (C.4) pour laquelle on ne néglige pas
le courant de déplacement, on obtient l'équation de continuité pour la densité de
charges :
Sous-sections
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
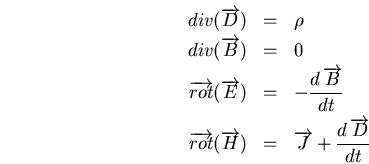
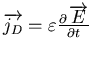 devant le
courant de conduction
devant le
courant de conduction