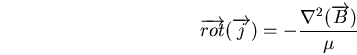C.2.2 Équation de la diffusion
D'après l'équation (C.4) et avec
 , on aC.8
pour un matériau isotropeC.9 :
, on aC.8
pour un matériau isotropeC.9 :
Donc en remplaçant
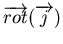 dans (C.6) dont on a pris le rotationnel, on obtient une expression pour
dans (C.6) dont on a pris le rotationnel, on obtient une expression pour
 que l'on remplace dans
l'équation de Maxwell (C.3). L'équation résultante décrit l'évolution du champ magnétique
que l'on remplace dans
l'équation de Maxwell (C.3). L'équation résultante décrit l'évolution du champ magnétique
 ;
c'est une équation de diffusion :
;
c'est une équation de diffusion :
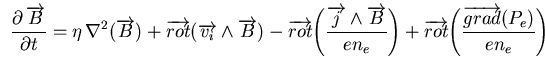 |
(C.7) |
avec

Notes
- ... aC.8
- On rappelle que
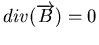
- ... isotropeC.9
- Ce qui permet de sortir
 et
et  des rotationnels
des rotationnels
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002