D.1.2 Définition macroscopique

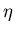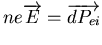Afin de comprendre à quoi correspond cette constante de proportionnalité $\eta$, on se place dans un état d'équilibre, qui est atteint lorsque les forces accélérant les électrons compensent juste les forces s'opposant à leur mouvement; c'est à dire lorsque^D.3 $n e \overrightarrow{E} = \overrightarrow{dP_{ei}}$. Or on vient d'établir que 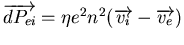$\overrightarrow{dP_{ei}} = \eta e^2 n^2 ( \overrightarrow{v_i} - \overrightarrow{v_e} )$ et par définition

$$\overrightarrow{j} = e n ( \overrightarrow{v_i} - \overrightarrow{v_e} )$$ (D.2)

Par conséquent

$$\overrightarrow{E} = \eta \overrightarrow{j} = \frac{\overrightarrow{j}}{\sigma}$$ (D.3)

La constante de proportionnalité 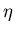$\eta$ entre le champ électrique $\overrightarrow{E}$ et le courant que cela implique est appelée résistivité^D.4. Selon la modélisation retenue pour les collisions (collisions de tout ou partie des électrons avec les ions, avec des neutres ...), voir même selon la dynamique des électrons entre deux chocs, les expressions disponibles pour la résistivité diffèrent. Un modèle de résistivité consiste alors en un modèle de collisions (quelles espèces sur quelles espèces, dans quelles limites ...) qui permet de calculer des sections efficaces d'interaction ; puis une statistique pour la fonction de distribution des expèces en présence (statistique de FERMI-DIRAC, équation de BOLTZMAN ...) ainsi qu'une fonction de distribution des vitesses. Certains modèles peuvent aussi être semi-empiriques, tandis que d'autres utilisent un modèle self-consistant mais nécessitent des calculs longs et coûteux. Enfin, chacun de ces modèles n'est applicable que dans un régime plasma bien précis.

Notes

... lorsque^D.3

cette expression n'est valable que lorsque le champs $\overrightarrow{E}$ peut être considéré comme constant sur un libre parcours moyen; c'est à dire qu'il faut que le libre parcours moyen électronique soit très inférieur aux dimensions du système. SPITZER dans [89] donne comme critère la fréquence d'évolution des champs très inférieure aux fréquences de collisions. Dans le cas de champs électriques de très hautes fréquences, l'épaisseur de peau classique peut devenir plus petite que le libre parcours moyen des électrons. Cet effet de peau anormal signifie la fin de la validité de la loi d'ohm.

... macroscopique^D.4

On notera 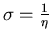$\sigma = \frac{1}{\eta}$ la conductivité