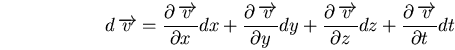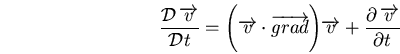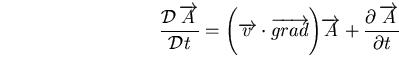C.1.2 Dérivée particulaire
Considérons un fluide composé de particules, par exemple une rivière. Si l'on s'intéresse à la vitesse d'une de ces particules, elle doit dépendre du
temps (évolution du débit de la rivière dans le temps), ainsi que de la position de la particule (prèsence d'un rapide
par exemple). Si l'on cherche l'accélération, on aura donc :
soit :
Le premier terme représente l'accélération de la particule dans le référentiel absolu, le terme
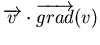 représente l'accélération vue par la particule du fait de son déplacement dans le champ de
vitesses, et le terme
représente l'accélération vue par la particule du fait de son déplacement dans le champ de
vitesses, et le terme
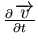 représente la variation de vitesse au cours du temps en
un point fixe de l'espace (il s'agit donc de l'altération du champ de vitesses au cours du temps).
La dérivée particulaire d'une grandeur
représente la variation de vitesse au cours du temps en
un point fixe de l'espace (il s'agit donc de l'altération du champ de vitesses au cours du temps).
La dérivée particulaire d'une grandeur
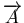 s'écrit donc :
s'écrit donc :
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002