Les champs électromagnétiques pénétrent d'une profondeur finie dans les matériaux
conducteurs non-idéauxE.1, dans le cadre de l'électromagnétisme
pur. Cette profondeur va définir le flux, l'énergie magnétique,
...présents dans le conducteur. De même, cette profondeur définira la résistance
électrique dynamique du matériau. Il importe donc de savoir la calculer et de
comprendre le phénomène pour traiter les problèmes courants en hautes puissances
pulsées en général et en compression de flux magnétique en particulier. Le traitement
présenté ici se limitera rapidement à un matériau à conductivité électrique  constante. Cette approximation est valable dans le cas où les densités de courants
sont suffisament faibles (voir
en section 2.3.2.1 page
constante. Cette approximation est valable dans le cas où les densités de courants
sont suffisament faibles (voir
en section 2.3.2.1 page ![[*]](./icons/crossref.png) pour un critère
permettant d'évaluer l'opportunité d'utiliser un tel modèle simplifié).
pour un critère
permettant d'évaluer l'opportunité d'utiliser un tel modèle simplifié).
Les phénomènes électromagnétiques purs sont décris par les
équations de Maxwell, auxquelles on applique
ensuite des conditions initiales, afin d'en obtenir une résolution. C'est pourquoi
nous allons étudier l'application de ces équations au cas que l'on souhaite traiter,
puis combiner ces équations entre elles dans l'approximation `` ondes
planes '',
c'est à dire la description des champs électriques et magnétiques par une ondeE.2 sous
la forme
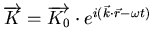 . Ceci permet ensuite d'exprimer la relation liant le vecteur d'onde et la
pulsation, la relation de dispersion (E.5). Dans le cas où le
vecteur d'onde est complexe, ceci signifie que l'onde subit un amortissement lors de
sa propagation. C'est un tel amortissement qui est caractéristique de l'effet de peau.
. Ceci permet ensuite d'exprimer la relation liant le vecteur d'onde et la
pulsation, la relation de dispersion (E.5). Dans le cas où le
vecteur d'onde est complexe, ceci signifie que l'onde subit un amortissement lors de
sa propagation. C'est un tel amortissement qui est caractéristique de l'effet de peau.
Notes
- ... non-idéauxE.1
- Dans le cadre de la magnétohydrodynamique, le
couplage entre une onde électromagnétique et une onde hydrodynamique permet une
propagation des champs sans atténuation dans un matériau de conductivité électrique
arbitraire ; c'est l'onde d'ALFVEN.
- ... ondeE.2
-
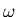 est la pulsation, telle
que
est la pulsation, telle
que
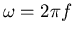 avec
avec  étant la fréquence et
étant la fréquence et 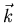 est le vecteur
d'onde
est le vecteur
d'onde
Sous-sections
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
![]() . Ceci permet ensuite d'exprimer la relation liant le vecteur d'onde et la
pulsation, la relation de dispersion (E.5). Dans le cas où le
vecteur d'onde est complexe, ceci signifie que l'onde subit un amortissement lors de
sa propagation. C'est un tel amortissement qui est caractéristique de l'effet de peau.
. Ceci permet ensuite d'exprimer la relation liant le vecteur d'onde et la
pulsation, la relation de dispersion (E.5). Dans le cas où le
vecteur d'onde est complexe, ceci signifie que l'onde subit un amortissement lors de
sa propagation. C'est un tel amortissement qui est caractéristique de l'effet de peau.