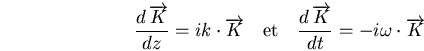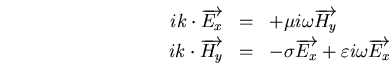E.1.2 Modélisation en ondes planes

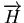Modélisons $\overrightarrow{E}$ et $\overrightarrow{H}$ par des ondes planes. Dans ce cas, les champs sont de la forme

$$\overrightarrow{E_x} = \overrightarrow{E_{x0}} \cdot e^{i(k... ...rrightarrow{H} = \overrightarrow{H_{x0}} \cdot e^{i(kz-wt)}$$

D'après cette modélisation, on a pour 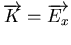$\overrightarrow{K} = \overrightarrow{E_x}$ ou $\overrightarrow{H_y}$

$$\frac{d \, {\overrightarrow{K}}}{d {z}} = ik \cdot \overrig... ...errightarrow{K}}}{d {t}} = -i \omega \cdot \overrightarrow{K}$$

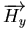
Ceci nous permet de ré-écrire (E.3) et (E.4) sous la forme

$$\begin{eqnarray*} ik \cdot \overrightarrow{E_x} & = & +\mu i \omega \overrighta... ...\overrightarrow{E_x} +\varepsilon i \omega \overrightarrow{E_x} \end{eqnarray*}$$

De ce système, nous en déduisons

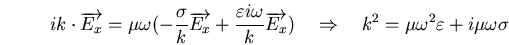$$ik \cdot \overrightarrow{E_x} = \mu \omega (-\frac{\sigma }... ...ow \quad k^2 = \mu \omega^2 \varepsilon + i \mu \omega \sigma$$ (E.5)

L'équation (E.5) est appellée relation de dispersion.