D.4.5 Modèle de LEE-MORE-DESJARLAIS

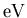Ce modèle, présenté dans [33], se propose d'étendre la plage de validité du modèle de LEE-MORE en traitant de façon plus fine le régime des plasmas denses, proches de la transition métal/isolant. Ainsi, les densités voisines de celle du solide et des températures de $0.5$ à plusieurs $\mathrm{eV}$ peuvent être traitées. Le but est d'intégrer des résultats théoriques récents et de soutenir la comparaison avec des données expérimentales récentes.

Figure: illustration sommaire du lissage retenu pour le calcul du degré d'ionisation dans le modèle de LEE-MORE-DESJARLAIS

Tout d'abord, le degré d'ionisation est calculé par la combinaison d'un modèle de THOMAS-FERMI et d'une loi de Saha modifiée pour prendre en compte l'influence de la pression. Cette correction en fonction de la pression est semi-empirique, et vient de comparaisons avec des modèles théoriques. On obtient une loi de SAHA sous la forme (voir équation C.35 page pour l'expression habituelle de la loi de SAHA):

$$K = \frac{2 g_1}{g_0} \frac{1}{n_\alpha} \frac{{(2 \pi m_e ... ... \frac{1.5 e^2}{E_i R_\alpha} \bigr)}^{\frac{3}{2}} \Bigr) }$$ (D.14)

Où $E_i$ est l'énergie de première ionisation, $R_\alpha$ est le rayon de Wigner-Seitz et le coefficient $1.5$ ainsi que l'exposant $\frac{3}{2}$ sont issus de comparaisons avec des calculs analytiques. Une pondération est appliquée à cette loi, $f_e = \frac{1}{2} ( \sqrt{K^2+4K}-K )$ et ceci est combiné avec un modèle d'ionisation de THOMAS-FERMI pour calculer le degré d'ionisation moyen

$$\bar{Z} = f_e^{\frac{2}{Z_{TF}^2}} Z_{TF} + \Biggl( 1 - f_e^{\frac{2}{Z_{TF}^2}} \Biggr) f_e$$ (D.15)

La figure D.5 présente les degrés d'ionisations évalués avec des modèles de SAHA, de THOMAS-FERMI et le lissage retenu dans le modèle de DESJARLAIS^D.20. Le calcul à partir du modèle de SAHA est fait en considérant $n_\alpha=n_{ions}$.

Ensuite, la section efficace d'interaction électrons/neutres est calculée dans l'approximation de BORN en se basant sur une section efficace de transfert de quantité de mouvement^D.21. Le calcul tel quel n'est pas intégré dans le modèle, mais plutôt une approximation du résultat. Le traitement des collisions électrons/électrons a été refait, les fonctions de FERMI et le potentiel chimique sont évalués dans l'approximation de ZIMMERMANN.

Enfin, la borne inférieure du taux de relaxation est redéfinie en accord avec des mesures expérimentales récentes (voir [30]) de façon à se comporter correctement en dessous de $1 \, \mathrm{eV}$.

Une version améliorée de ce modèle existe, il s'agit d'un complément prenant en compte la structure en bandes d'énergies des ions (donc celà permet de calculer une résistivité dépendant de la fréquence, dont on ne retiendra que la partie continue) ainsi que la structure de la maille cristalline. Un calcul de dynamique moléculaire^D.22est alors mené, et les résultats sont réintégrés dans les tables précédement établies.

Notes

...Desjarlais^D.20

Sources de ces modèles: [33] et [31]

... mouvement^D.21

En régime de faible ionisation, la différence par rapport à la section efficace électrons/neutres constante du modèle de LEE-MORE est assez importante.

... moléculaire^D.22

Pour un tel calcul, on simule le mouvement des ions sur quelques mailles cristallines. Les pas de temps sont de l'ordre de quelques $\mathrm{fs}$.