D.5 Comparaison de modèles de résistivité: cas de l'aluminium

Figure: comparaison de modèles de résistivité pour l'aluminium - pour différentes densités, en $\mathrm{kg/m^3}$

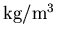
Il est maintenant intéressant de comparer les résultats produits par différents modèles. La comparaison est faite pour de l'aluminium, du fait de son intérêt pour la compression de flux, et du fait de son faible numéro atomique, ce qui permet une diffusion large et non restreinte de ces données. Sur la figure D.6, les profils de conductivité en fonction de la température sont représentés pour différentes densités, avec un code de couleur qui est le même pour les différents modèles. La première courbe est issue des données extraites de la table SESAME 23714, c'est à dire un modèle de RINKER. Un calcule de la rrésistivité de SPITZER est superposé, pour $\rho=1 \, \mathrm{kg/m^3}$, le degré d'ionisation en fonction de la température étant celui fourni par cette table. Une seconde courbe représente le contenu d'une table basée sur un modèle de HARTREE-FOCK-SLATER et sur des interpolations de modèles analytiques^D.23 en dessous de $1 \, \mathrm{eV}$ (source: [21]). Le calcul de SPITZER est réalisé avec le degré d'ionisation précédement extrait des tables SESAME . Enfin, la résistivité de LEE-MORE-DESJARLAIS (source [31]) est tracée, la même remarque que précédement s'applique sur la résistivité de SPITZER. Ce modèle est très proche des valeurs des formulaires pour la résistivité de l'aluminium à température ambiante et densité usuelle.

Il faut retenir de cette comparaison que pour des températures supérieures à 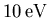$10 \, \mathrm{eV}$ et des densités inférieures à celle du solide, tout les modèles convergent vers le modèle de SPITZER.

Notes

... analytiques^D.23

Les températures de fusion sont ainsi fixées dans ces modèles, ce qui explique qu'il n'y ait visiblement pas de dépendance de celles-ci avec la densité. De plus, le point d'inflexion correspondant paraît être trop marqué, d'après une réflexion de M. DESJARLAIS.