C.5.2 Plasma en équilibre thermodynamique, plasma hors
équilibre
Sous l'effet de l'agitation thermique, des collisions ionisent les ions. Si les processus de recombinaison entre électrons
et ions équilibrent cette ionisation, le plasma est en équilibre thermodynamique : l'ionisation est déterminée par la
pression et la température. Dans le cas d'un gaz monoatomique, on peut appliquer la
loi de SAHA :
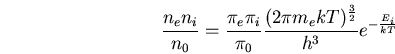 |
(C.35) |
Où  représente l'énergie d'ionisation du gaz, et
représente l'énergie d'ionisation du gaz, et 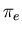 ,
, 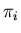 ,
, 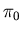 les poids statistiques des électrons, ions
et neutres. Les
les poids statistiques des électrons, ions
et neutres. Les  représentent des nombres de particules par unité de volume.
Si les processus de recombinaisons n'équilibrent pas les processus d'ionisations, le plasma est hors d'équilibre
thermodynamique.
Un état stationnaire atteint par le plasma peut être décrit par son degré d'ionisation
représentent des nombres de particules par unité de volume.
Si les processus de recombinaisons n'équilibrent pas les processus d'ionisations, le plasma est hors d'équilibre
thermodynamique.
Un état stationnaire atteint par le plasma peut être décrit par son degré d'ionisation 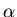 , les nombres de particules
par unité de volume
, les nombres de particules
par unité de volume  pour chaque espèce (électrons, ions, neutres), et les températures
pour chaque espèce (électrons, ions, neutres), et les températures  pour chaque espèce
également.
Ainsi, si un plasma à l'équilibre thermodynamique est un plasma décrit par une distribution indépendante du temps et de
l'espace, il est possible de décrire un équilibre thermodynamique local : dans ce cas, il existe des écarts à l'équilibre
(par exemple une densité ou une température non uniforme), mais le temps caractéristique de retour à l'équilibre est petit
devant le temps caractéristique des mécanismes qui perturbent le milieu (et le même raisonnement doit s'appliquer aussi aux
distances caractéristiques des perturbations devant le libre parcours moyen).
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
pour chaque espèce
également.
Ainsi, si un plasma à l'équilibre thermodynamique est un plasma décrit par une distribution indépendante du temps et de
l'espace, il est possible de décrire un équilibre thermodynamique local : dans ce cas, il existe des écarts à l'équilibre
(par exemple une densité ou une température non uniforme), mais le temps caractéristique de retour à l'équilibre est petit
devant le temps caractéristique des mécanismes qui perturbent le milieu (et le même raisonnement doit s'appliquer aussi aux
distances caractéristiques des perturbations devant le libre parcours moyen).
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002