Le modèle de ZIMAN décrit le matériau comme un milieu homogène (potentiel
uniforme) renfermant des centres de diffraction sphériques, mutuellement
impénétrables (c'est à dire sans
recouvrement) et statistiquement distribuésD.12(c'est à dire que le système est désordonné, donc des interactions électrons/phonons
ne peuvent pas être prises en compte). Cette distribution statistique rend
possible la corrélation entre les positions de deux centres de diffraction par la
fonction de corrélationD.13
 .
Les collisions sont des collisions à deux corps, chaque électron interagissant avec
un seul ion à la fois. De plus, ce modèle utilise l'approximation du libre parcours
moyen, qui constiste à considérer que les électrons sont accélérés sur un libre
parcours moyen
.
Les collisions sont des collisions à deux corps, chaque électron interagissant avec
un seul ion à la fois. De plus, ce modèle utilise l'approximation du libre parcours
moyen, qui constiste à considérer que les électrons sont accélérés sur un libre
parcours moyen  (voir note 15) avant de subir une
collision dissipant la totalité de leur énergie cinétique, puis ré-accélérés et ainsi
de suite.
Les électrons libres considérés comme responsables de la conduction sont les
électrons de valence, les électrons de c
(voir note 15) avant de subir une
collision dissipant la totalité de leur énergie cinétique, puis ré-accélérés et ainsi
de suite.
Les électrons libres considérés comme responsables de la conduction sont les
électrons de valence, les électrons de c ur étant négligés. Enfin, la force
résultant de l'application d'un champ électrique à ce modèle est linéarisée en
fonction de la densité de courant et identifiée à
ur étant négligés. Enfin, la force
résultant de l'application d'un champ électrique à ce modèle est linéarisée en
fonction de la densité de courant et identifiée à
 . On suppose alors
implicitement que la diffraction d'un électron ne se fait que sur un centre de
diffraction à la fois, ce qui n'est pas toujours justifiéD.14. La
résitivité est alors calculée de la façon suivante (formulation matricielle par
EVANS, voir [36]):
. On suppose alors
implicitement que la diffraction d'un électron ne se fait que sur un centre de
diffraction à la fois, ce qui n'est pas toujours justifiéD.14. La
résitivité est alors calculée de la façon suivante (formulation matricielle par
EVANS, voir [36]):
 |
(D.8) |
Le premier terme est lié à l'ionisation (électrons de valence), le second signifie
que les électrons responsables de la conduction suivent une statistique de
FERMI-DIRAC et le troisième terme représente les interactions entre
électrons et centre diffuseursD.15. C'est ce dernier terme qui est à
l'origine du logarithme coulombien, que le modèle de SPITZER évalue
exactement mais dans une plage tronquée de façon à éviter sa divergence.
Dans cette expression,
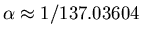 est la constante de structure
fine,
est la constante de structure
fine,  le volume atomique,
le volume atomique,  le degré d'ionisation ,
le degré d'ionisation ,
 la fonction de
distribution de FERMI-DIRAC,
la fonction de
distribution de FERMI-DIRAC,  l'énergie,
l'énergie,  le potentiel
chimique,
le potentiel
chimique,
 la section efficace d'interaction
électrons-ions et
la section efficace d'interaction
électrons-ions et  la quantité de mouvement.
la quantité de mouvement.  étant le facteur de
structure (voir l'explication en note 13). Cette grandeur est donc représentative du potentiel établi par les
centres diffuseurs (voir section D.2.1).
étant le facteur de
structure (voir l'explication en note 13). Cette grandeur est donc représentative du potentiel établi par les
centres diffuseurs (voir section D.2.1).
Les interactions électrons-ions sont traitées comme des collisions à deux corps, ce
qui limite la plage de validité de ce modèle. De plus, cette expression est
explicitement non relativiste, donc à priori non applicable aux électrons de trop
grande énergie. Les paramètres devant être tabulés sont la section efficace
 , la densité d'électrons libres
, la densité d'électrons libres  , ainsi que
des modèles de facteurs de structure décrivant les corrélations ions/ions. C'est
pourquoi ce modèle est particulièrement approprié pour les métaux liquides, matériaux
pour lesquels de telles données sont connues précisémentD.16.
, ainsi que
des modèles de facteurs de structure décrivant les corrélations ions/ions. C'est
pourquoi ce modèle est particulièrement approprié pour les métaux liquides, matériaux
pour lesquels de telles données sont connues précisémentD.16.
Notes
- ... distribuéD.12
- Ce modèle est défini pour un
liquide, et c'est uniquement par extrapolation qu'il est utilisé pour un plasma.
- ... corrélationD.13
- En fait, il s'agit d'un abus de langage : on
devrait plutôt parler de fonction de paire,
la fonction de corrélation étant la
fonction
 (il est vrai, basée sur la fonction de paire) telle que le
facteur de structure
(il est vrai, basée sur la fonction de paire) telle que le
facteur de structure
 avec
avec  la matrice identité. La fonction de paire est
représentative du potentiel établi par les centres diffuseurs (voir section
D.2.1), et permet de calculer la fonction de corrélation dont
le facteur de structure est la transformée de Fourrier.
la matrice identité. La fonction de paire est
représentative du potentiel établi par les centres diffuseurs (voir section
D.2.1), et permet de calculer la fonction de corrélation dont
le facteur de structure est la transformée de Fourrier.
- ... justifiéD.14
- Dans le cas d'un
plasma trop fortement corrélé, cette approximation n'est plus valable.
- ... diffuseursD.15
- Celles-ci sont représentées par le libre
parcours moyen qui dépend de l'ordre de grandeur de la distance ionique calculée à
partir du facteur de structure
 (évidemment, ces interactions sont
pondérées par la section efficace
(évidemment, ces interactions sont
pondérées par la section efficace
 ). D'après la théorie de
ZIMAN, le libre parcours moyen s'exprime:
). D'après la théorie de
ZIMAN, le libre parcours moyen s'exprime:
avec  l'angle de diffraction et
l'angle de diffraction et
 la section efficace
différentielle (voir [98]).
la section efficace
différentielle (voir [98]).
- ... précisémentD.16
- De plus, un métal
liquide présente une densité assez élevée, donc les interactions sont le plus
fréquemment à courte distance, ce qui se traduit par des interactions plutôt à deux
corps. En effet, dans le cas d'une interaction à courte distance, du fait de la forme
du potentiel coulombien (en
 ), l'influence des autres corps est très réduite
par rapport à l'intensité de la force qui s'exerce entre les deux corps les plus
proches.
), l'influence des autres corps est très réduite
par rapport à l'intensité de la force qui s'exerce entre les deux corps les plus
proches.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
![]() est la constante de structure
fine,
est la constante de structure
fine, ![]() le volume atomique,
le volume atomique, ![]() le degré d'ionisation ,
le degré d'ionisation ,
![]() la fonction de
distribution de FERMI-DIRAC,
la fonction de
distribution de FERMI-DIRAC, ![]() l'énergie,
l'énergie, ![]() le potentiel
chimique,
le potentiel
chimique,
![]() la section efficace d'interaction
électrons-ions et
la section efficace d'interaction
électrons-ions et ![]() la quantité de mouvement.
la quantité de mouvement. ![]() étant le facteur de
structure (voir l'explication en note 13). Cette grandeur est donc représentative du potentiel établi par les
centres diffuseurs (voir section D.2.1).
étant le facteur de
structure (voir l'explication en note 13). Cette grandeur est donc représentative du potentiel établi par les
centres diffuseurs (voir section D.2.1).
![]() , la densité d'électrons libres
, la densité d'électrons libres ![]() , ainsi que
des modèles de facteurs de structure décrivant les corrélations ions/ions. C'est
pourquoi ce modèle est particulièrement approprié pour les métaux liquides, matériaux
pour lesquels de telles données sont connues précisémentD.16.
, ainsi que
des modèles de facteurs de structure décrivant les corrélations ions/ions. C'est
pourquoi ce modèle est particulièrement approprié pour les métaux liquides, matériaux
pour lesquels de telles données sont connues précisémentD.16.