C.3.5 Équation thermique
Si l'on note
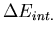 l'énergie interne d'un élément de volume de plasma
l'énergie interne d'un élément de volume de plasma
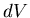 et
et 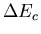 son énergie cinétique,
le bilan énergétique s'écritC.13
son énergie cinétique,
le bilan énergétique s'écritC.13
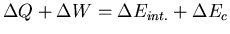 .
Du point de vue des électrons, l'énergie peut être échangée via différents moyens
(les quantités d'énergie sont exprimées localement et pour un volume
.
Du point de vue des électrons, l'énergie peut être échangée via différents moyens
(les quantités d'énergie sont exprimées localement et pour un volume 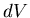 de hauteur
de hauteur
 , de longueur
, de longueur  et d'épaisseur
et d'épaisseur 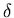 ):
):
- par les champs électromagnétiques. Ceci s'écrit
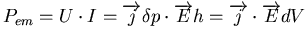 . Ensuite, on détaillera ceci en
utilisant une loi d'OhmC.14.
. Ensuite, on détaillera ceci en
utilisant une loi d'OhmC.14.
- par les photons sous la forme de rayonnement. On notera
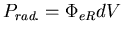 .
.
- par le travail des forces s'exerçant sur le petit élément de fluide. On ne
retiendra que le
travail des forces de pression, défini par
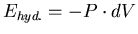 . La puissance
apportée par les forces de pression se calcule donc à partir de la dérivée de
cette énergie. Mais il faut remarquer qu'une variation de pression ne produit pas
de travailC.15: c'est
uniquement la variation du volume qui contribue au travail des forces de
pression. Ainsi
. La puissance
apportée par les forces de pression se calcule donc à partir de la dérivée de
cette énergie. Mais il faut remarquer qu'une variation de pression ne produit pas
de travailC.15: c'est
uniquement la variation du volume qui contribue au travail des forces de
pression. Ainsi
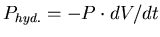 . Si l'on raisonne en une dimension, le
coté ayant une vitesse
. Si l'on raisonne en une dimension, le
coté ayant une vitesse
 par rapport au reste de l'élément de volume
par rapport au reste de l'élément de volume 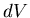 apporte une contribution
apporte une contribution
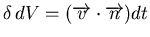 (
(
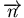 étant la normale à la surface). Pour un élément de volume tridimensionel,
il suffit alors d'ajouter les contributions des différentes faces, c'est à dire
d'intégrer cette quantité
étant la normale à la surface). Pour un élément de volume tridimensionel,
il suffit alors d'ajouter les contributions des différentes faces, c'est à dire
d'intégrer cette quantité 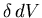 sur l'élément de surface
sur l'élément de surface  du volume
du volume
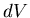 . Ceci représente alors une divergence (voir C.1.1.2), donc on à:
. Ceci représente alors une divergence (voir C.1.1.2), donc on à:
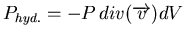 .
.
- par des processus de conduction de la chaleur (collisions entre particules
de même nature). La puissance conduite s'exprime habituellement sous la forme
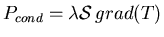 ;
;  étant le coefficient
de conductibilité thermique. Étant donné que l'on raisonne localement, il faut
intégrer ce flux d'énergie sur l'ensemble de la surface de l'élément de volume
(l'énergie est conduite via toute la surface de l'élément) ;
ce qui revient à
étant le coefficient
de conductibilité thermique. Étant donné que l'on raisonne localement, il faut
intégrer ce flux d'énergie sur l'ensemble de la surface de l'élément de volume
(l'énergie est conduite via toute la surface de l'élément) ;
ce qui revient à
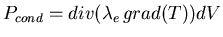 .
.
- par les collisions microscopiques entre particules de nature différente. Il
s'agit du chauffage d'un gaz de particules
 par un gaz de particules
par un gaz de particules
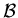 . En raisonnant à volume constant, la variation d'énergie produite
par une variation de température s'écrit:
. En raisonnant à volume constant, la variation d'énergie produite
par une variation de température s'écrit: 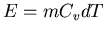 . Si l'on considère que
les électrons passent de la température
. Si l'on considère que
les électrons passent de la température  à la température
à la température  en un temps
en un temps
 , alors la puissance échangée s'écrit:
, alors la puissance échangée s'écrit:
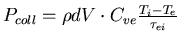 .
.
Utilisons la loi d'Ohm généralisée (C.6) pour
 , en remarquant que
, en remarquant que
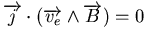 car
car
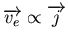 .
Si l'on considère que les électrons n'ont pas de masseC.16, l'énergie
cinétique est nulle (ce qui est cohérent avec le fait que le terme en
.
Si l'on considère que les électrons n'ont pas de masseC.16, l'énergie
cinétique est nulle (ce qui est cohérent avec le fait que le terme en
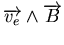 n'apporte aucune contribution énergétique).
La conservation de l'énergie s'écrit donc, pour les électrons:
n'apporte aucune contribution énergétique).
La conservation de l'énergie s'écrit donc, pour les électrons:
Dans le cas où l'on utilise une viscosité numérique, on
remplace la pression
 par le terme
par le terme 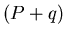 ,
,  étant le terme dissipatif numérique (voir
section H.1.7 page
étant le terme dissipatif numérique (voir
section H.1.7 page ![[*]](./icons/crossref.png) ).
Pour les ions, on peut construire le même type d'équation, mais l'énergie cinétique
sera prise en compte, le terme en
).
Pour les ions, on peut construire le même type d'équation, mais l'énergie cinétique
sera prise en compte, le terme en
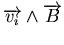 apportera une
contribution et les termes de rayonnement et de chauffage ohmiqueC.17 pourront être négligés.
apportera une
contribution et les termes de rayonnement et de chauffage ohmiqueC.17 pourront être négligés.
Notes
- ... s'écritC.13
- Avec
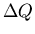 étant la quantité de chaleur échangée, et
étant la quantité de chaleur échangée, et 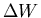 étant le travail échangé
étant le travail échangé
- ... d'OhmC.14
- Pour un pinch, c'est ce terme qui est la
source d'énergie, les autres formes résultant de la transformation de l'énergie
électrique.
- ... travailC.15
- Mais une variation d'énergie interne se traduit par une
variation de pression: un plasma chauffé augmentera sa pression
- ... masseC.16
- Ceci permet de rester
cohérent avec l'approximation que le courant est uniquement porté par les électrons:
en effet, cette approximation suppose que les vitesses électroniques sont très
grandes devant les vitesses ioniques, du fait de la très faible masse des électrons
devant celle des ions.
- ... ohmiqueC.17
- Ceci
revient à négliger le courant ionique.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002