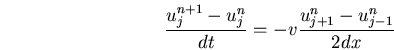H.1.4 Difficulté de la résolution de la convection
Lorsque l'on veut résoudre une équation telle que la loi de conservation de
la masse pour un fluide ..., on doit résoudre une équation qui en
1D
est de la formeH.2 :
avec  une fonction arbitraire des grandeurs temporelles et spatiales
une fonction arbitraire des grandeurs temporelles et spatiales
 et
et 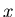 .
Une méthode de résolution explicite conduirait à :
.
Une méthode de résolution explicite conduirait à :
soit, en regroupant les termes (ce qui permet de retrouver une forme
habituelle pour un calcul explicite) :
Supposons que  varie selon
varie selon
 . Alors après simplification par
. Alors après simplification par
 (afin de connaître le taux d'amplification de
(afin de connaître le taux d'amplification de  , il faut
diviser
, il faut
diviser  par
par  ) l'expression précédente s'écrit :
) l'expression précédente s'écrit :
Ainsi, en un pas de temps,  est multipliée par
est multipliée par
 . Le taux d'amplification est
alors :
. Le taux d'amplification est
alors :
Ceci signifie que la résolution de la convection par une méthode explicite
est divergente. C'est pourquoi l'hydrodynamique est en général résolue de
façon implicite par les codes MHD
H.3 (voir en section H.1.6 pour ce que cela implique).
Notes
- ... formeH.2
- le cas 1D
a été choisi pour des raisons
de simplicité, le raisonnement qui va suivre est tout aussi valable dans
d'autres dimensions.
- ... MHDH.3
- pour plus de précisions,
et un exposé des autres méthodes numériques disponibles, on peut se réfèrer
à [90]
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002