H.1.6 Résolution de la diffusion du champ magnétique
L'équation de diffusion du champ magnétique
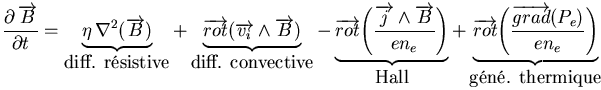 |
(H.1) |
est découpée en plusieurs partie avant sa résolution par Mach2
H.4 : ainsi, l'équation de diffusion résistive
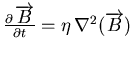 est résolue par la routine magdiff. Ensuite, c'est
l'équation de l'effet HALL
est résolue par la routine magdiff. Ensuite, c'est
l'équation de l'effet HALL
 qui est résolue par la routine hall. Puis, la routine thmag résoud
l'équation de génération thermique de champ magnétique. Enfin, c'est au tour de l'équation de la diffusion
convective, via les routines hyditblk, trnslp et hydwgrdb.
Le but de ce découpage est de permettre une résolution de la diffusion résistive implicite (en effet, la grande valeur
possible pour la diffusivité
qui est résolue par la routine hall. Puis, la routine thmag résoud
l'équation de génération thermique de champ magnétique. Enfin, c'est au tour de l'équation de la diffusion
convective, via les routines hyditblk, trnslp et hydwgrdb.
Le but de ce découpage est de permettre une résolution de la diffusion résistive implicite (en effet, la grande valeur
possible pour la diffusivité 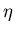 imposerait un pas de temps très petit dans le cas d'une méthode expliciteH.5). Les autres équations régissant l'évolution du champ magétique peuvent quant à
elles être résolues par des méthodes explicites sans difficultés. Par contre la mise en commun de ces résultats partiels peut
être une source d'instabilité numérique lors de la convergence de la résolution de la diffusion de
imposerait un pas de temps très petit dans le cas d'une méthode expliciteH.5). Les autres équations régissant l'évolution du champ magétique peuvent quant à
elles être résolues par des méthodes explicites sans difficultés. Par contre la mise en commun de ces résultats partiels peut
être une source d'instabilité numérique lors de la convergence de la résolution de la diffusion de
 au sens
largeH.6.
au sens
largeH.6.
Notes
- ... Mach2H.4
- d'après
[43], [19] et [21]
- ... expliciteH.5
- ne
pas oublier le lien existant entre la diffusivité physique et la diffusivité numérique : il faut toujours
 pour que le calcul soit correct.
pour que le calcul soit correct.
- ...
largeH.6
- une méthode de résolution de l'équation de diffusion du champ magnétique en un seul bloc existe, elle est
utilisée dans certains codes (MHDR
de Los Alamos Natl. Lab. par exemple) mais ceci impose une résolution implicite de
cette équation ainsi que des équations hydrodynamiques.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
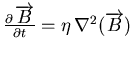 est résolue par la routine magdiff. Ensuite, c'est
l'équation de l'effet HALL
est résolue par la routine magdiff. Ensuite, c'est
l'équation de l'effet HALL
 qui est résolue par la routine hall. Puis, la routine thmag résoud
l'équation de génération thermique de champ magnétique. Enfin, c'est au tour de l'équation de la diffusion
convective, via les routines hyditblk, trnslp et hydwgrdb.
Le but de ce découpage est de permettre une résolution de la diffusion résistive implicite (en effet, la grande valeur
possible pour la diffusivité
qui est résolue par la routine hall. Puis, la routine thmag résoud
l'équation de génération thermique de champ magnétique. Enfin, c'est au tour de l'équation de la diffusion
convective, via les routines hyditblk, trnslp et hydwgrdb.
Le but de ce découpage est de permettre une résolution de la diffusion résistive implicite (en effet, la grande valeur
possible pour la diffusivité