H.1.3 Méthode implicite, explicite, semi-implicite
Il s'agit de méthodes de résolution d'équations différentielles de la forme :
La méthode explicite calcule
 en fonction de
en fonction de
 et aussi des termes
et aussi des termes
 et
et
 . Il s'agit donc de
l'évaluation de la dérivée à droite en
. Il s'agit donc de
l'évaluation de la dérivée à droite en  et centrée en
et centrée en 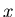 .
Cette méthode est rapide, mais instable si le pas de temps n'est pas suffisamment petit :
.
Cette méthode est rapide, mais instable si le pas de temps n'est pas suffisamment petit :

Sinon, une petite différence sur les conditions initiales risque de se traduire par une grande différence sur la
solution approchée.
La méthode implicite calcule
 en fonction
de
en fonction
de
 mais aussi des termes
mais aussi des termes
 et
et
 .
Cette méthode est lente (calcul matriciel), mais universellement stable (le facteur limitant de
.
Cette méthode est lente (calcul matriciel), mais universellement stable (le facteur limitant de  concerne les
erreurs de troncature). Il s'agit alors de l'évaluation de la dérivée à gauche en
concerne les
erreurs de troncature). Il s'agit alors de l'évaluation de la dérivée à gauche en  et centrée en
et centrée en 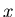 .
On fait alors la moyenne des deux évaluations à droite et à gauche en
.
On fait alors la moyenne des deux évaluations à droite et à gauche en  de
de
 , afin de calculer
, afin de calculer
 centré en
centré en
 . Cette
méthode est la méthode de
Crank-Nicholson, ou bien semi implicite (voir fig H.1, et référence [73]). Toutes ces
méthodes peuvent en fait s'exprimer de façon unique en fonction d'un paramètre
. Cette
méthode est la méthode de
Crank-Nicholson, ou bien semi implicite (voir fig H.1, et référence [73]). Toutes ces
méthodes peuvent en fait s'exprimer de façon unique en fonction d'un paramètre  (c'est le paramètre
d'implicité) qui désigne une méthode explicite (
(c'est le paramètre
d'implicité) qui désigne une méthode explicite ( ), implicite (
), implicite (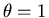 ) ou Cranck-Nicholson (
) ou Cranck-Nicholson (
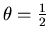 ).
).
Figure:
méthodes explicites, implicites, semi-implicites
|
|
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
