Reprenons l'équation de diffusion (E.9). Considèrons un signal
de temps caractéristique  et d'amplitude
et d'amplitude  appliqué sur la surface de
l'échantillon conducteur de diffusivité
appliqué sur la surface de
l'échantillon conducteur de diffusivité 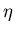 . Le signal
. Le signal
 étant appliqué à la surface de l'échantillon, si l'on se place au temps
étant appliqué à la surface de l'échantillon, si l'on se place au temps
 et à la distance
et à la distance
 , alors on peut ré-écrire
l'équation sous la forme normalisée :
, alors on peut ré-écrire
l'équation sous la forme normalisée :
Il faut que
 soit une longueur caractéristique du problème pour que
la normalisation par celle-ci ait un sens physique. Prenons donc une approximation de
l'épaisseur de peau en réponse à une rampe de courant à
soit une longueur caractéristique du problème pour que
la normalisation par celle-ci ait un sens physique. Prenons donc une approximation de
l'épaisseur de peau en réponse à une rampe de courant à 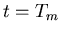 (voir
[8])
(voir
[8])
 . Ceci permet
alors d'écrire l'équation de la diffusion plane sous la formeE.9 :
. Ceci permet
alors d'écrire l'équation de la diffusion plane sous la formeE.9 :
 |
(E.12) |
L'équation (E.12) signifie donc que l'on peut définir une classe
de problèmes ayant une même forme de signal appliqué à la surface du matériau au cours
du temps, qui possédera une solution normalisée unique qu'il suffit ensuite de
multiplier par les paramètres de la normalisation du problème précis que l'on
souhaite résoudre. Par exemple, si l'on résout le profil spatial de champ
magnétique pour un signal sinusoïdal de quart de période
 à
à
 dans du cuivre, il sera possible d'en déduire le même profil spatial pour
un quart de période de
dans du cuivre, il sera possible d'en déduire le même profil spatial pour
un quart de période de
 dans du manganèse !
dans du manganèse !
Notes
- ... formeE.9
- On rappelle
que

Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
