Dans le cas plan, il est possible de transformer l'équation (E.8) en
 |
(E.9) |
Utilisons le changement de variables
 .
Ce choix peut être justifié plus ou moins physiquement: en effet, lors de la
diffusion d'un champ dans un conducteur, ce champ
doit s'affaiblir avec la profondeur de pénétration, mais il doit augmenter avec le
temps. Toutefois, il est nécessaire
que l'influence du temps soit moins forte que celle de la profondeur afin que
.
Ce choix peut être justifié plus ou moins physiquement: en effet, lors de la
diffusion d'un champ dans un conducteur, ce champ
doit s'affaiblir avec la profondeur de pénétration, mais il doit augmenter avec le
temps. Toutefois, il est nécessaire
que l'influence du temps soit moins forte que celle de la profondeur afin que
 quel que soit
quel que soit  . Une
analyse dimentionnelle permet de confirmer ceci et de choisir un champ sous la
forme
. Une
analyse dimentionnelle permet de confirmer ceci et de choisir un champ sous la
forme
 . Le facteur
. Le facteur
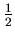 n'est justifié que par des facilités de calcul.
On en déduit
n'est justifié que par des facilités de calcul.
On en déduit
d'où
donc en simplifiant et en posant
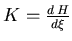 , alors l'équation
, alors l'équation
de solution
conduit à la solution générale pour  :
:
Sous-sections
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002


