E.2.1 Nécessité de la prise en compte de la diffusion

Considérons encore une fois (E.1) et (E.2). Nous obtenons donc dans le cas d'un bon conducteur ( $\sigma \overrightarrow{E} \gg \varepsilon \frac{d \, {\overrightarrow{E}}}{d {t}}$ )

$\begin{displaymath} \left\{ \begin{array}{rcl} \mathop{\overrightarrow{rot}}(... ...w{{H}}) & = & \sigma \overrightarrow{E} \end{array} \right. \end{displaymath}$

d'où

$\begin{displaymath} \overrightarrow{\mathop{rot}}(\mathop{\overrightarrow{rot}}... ...tarrow{{H}})) = - \mu \frac{d \, {\overrightarrow{H}}}{d {t}} \end{displaymath}$

Or $\overrightarrow{\mathop{rot}}(\mathop{\overrightarrow{rot}}(\overrightarrow{{A}... ...\mathop{grad}}(\mathop{div}(\overrightarrow{A})) - \nabla^2(\overrightarrow{A})$ et de plus $\overrightarrow{\mathop{grad}}(\mathop{div}(\overrightarrow{H})) = \overrightarrow{0}$ donc nous avons l'équation différentielle suivante:

$\begin{displaymath} \nabla^2 \overrightarrow{H} = \mu \sigma \frac{d \, {\overrightarrow{H}}}{d {t}} \end{displaymath}$

(E.8)

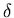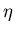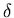Ceci est une équation de diffusion de coefficient de diffusion $\eta = \frac{1}{\mu \sigma}$ . Soit $\tau$ un temps caractéristique repésentant le temps que le champ diffuse jusqu'à une profondeur $\delta$ (épaisseur de peau). Etant donné que le coefficient de diffusion $\eta$ représente une vitesse de diffusion et que $\delta$ représente une distance, il est possible d'en déduire une expression^E.7 de $\tau$ . 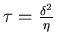L'expression retenue est donc $\tau = \frac{\delta^2}{\eta}$ ce qui permet d'après l'expression de 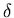$\delta$ donnée en note 6 pour un conducteur idéal d'exprimer $\tau$ sous la forme $\tau = \frac{1}{\pi f}$ .

Dans le cas d'un signal sous la forme d'un quart de sinusoïde (cas le plus fréquent pour les générateurs de hautes puissances pulsées), le temps de pénétration $\tau$ est voisin de la durée de l'impulsion. Il est donc nécessaire de prendre en compte la diffusion des champs dans le conducteur.

Notes

... expression ^E.7: Celle-ci peut aussi être établie par un raisonnement aux dimensions.

Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002