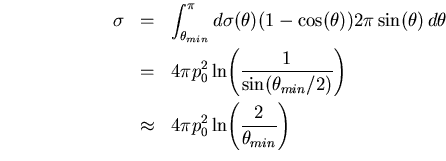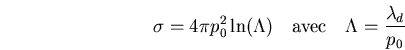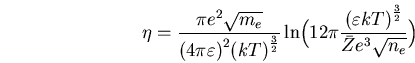D.3.1 Calcul de la fréquence de collision
Figure D.3:
collision coulombienne
|
|
Lors d'une collision d'un électron sur un ion immobile
(on fait l'hypothèse d'un gaz de
LorentzD.7), une force coulombienne
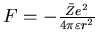 dévie l'électron. Soit
dévie l'électron. Soit  le paramètre d'impact, et
le paramètre d'impact, et  l'angle de déviation
(voir figure D.3). Calculons le paramètre d'impact critique, c'est à dire
l'angle de déviation
(voir figure D.3). Calculons le paramètre d'impact critique, c'est à dire  tel que
tel que
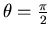 : du fait de la forte déviation, il s'agit d'une collision proche, donc on peut considérer que la force
coulombienne s'exerce pendant un temps
: du fait de la forte déviation, il s'agit d'une collision proche, donc on peut considérer que la force
coulombienne s'exerce pendant un temps
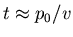 . Ceci modifie la quantité de mouvement de l'électron d'une
quantité
. Ceci modifie la quantité de mouvement de l'électron d'une
quantité
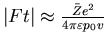 , qui doit être de
l'ordre de la quantité de mouvement
, qui doit être de
l'ordre de la quantité de mouvement 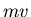 elle-même; donc
elle-même; donc
On a aussi la relation
La section efficace différentielle de collision élastique est donnée par la formule de Rutherford :
Il suffit d'intégrer ceci sur l'angle solide
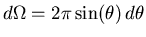 après l'avoir multiplié par
après l'avoir multiplié par
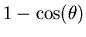 (qui représente la fraction de moment cinétique longitudinal échangé entre l'électron et l'ion) pour
obtenir la section efficace de transfert de quantité de mouvement :
(qui représente la fraction de moment cinétique longitudinal échangé entre l'électron et l'ion) pour
obtenir la section efficace de transfert de quantité de mouvement :
On peut faire l'approximation que
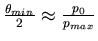 ,
, 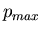 représentant le paramètre
d'impact maximum au delà duquel l'électron n'est plus soumis à la force coulombienne crée par l'ion. Ce paramètre d'impact
maximum est donc de l'ordre de la longueur de Debye lorsque le plasma est
suffisamment dense (voir section C.4.6 page
représentant le paramètre
d'impact maximum au delà duquel l'électron n'est plus soumis à la force coulombienne crée par l'ion. Ce paramètre d'impact
maximum est donc de l'ordre de la longueur de Debye lorsque le plasma est
suffisamment dense (voir section C.4.6 page ![[*]](./icons/crossref.png) pour plus de précisions sur l'écrantage de Debye). La section
efficace de transfert de quantité de mouvement est alors :
pour plus de précisions sur l'écrantage de Debye). La section
efficace de transfert de quantité de mouvement est alors :
Ceci permet à l'aide de l'équation (D.1) et en sachant que
 , d'exprimer la résistivitéD.8 SPITZER
, d'exprimer la résistivitéD.8 SPITZER 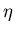 :
:
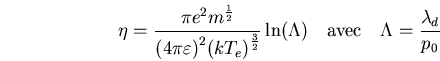 |
(D.6) |
Le logarithme coulombien  vaut en général
entre 10 et 20D.9.
vaut en général
entre 10 et 20D.9.
Notes
- ...
LorentzD.7
- Un gaz de Lorentz est un gaz totalement ionisé, dans lequel les
électrons n'interagissent pas entre eux mais uniquement avec des ions tous au repos.
- ... résistivitéD.8
- Voir [89] pour plus de
détails sur la démonstration
- ... 20D.9
- On peut retenir l'expression suivante pour la résistivité de
SPITZER:
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002