C.4.6 Longueur de DEBYE
Supposons un plasma globalement neutre. On décrit ce plasma comme un gaz d'électrons à la température  interagissant
avec des ions sous forme de particules aléatoirement distribuées. Le nuage électronique supposé en équilibre
thermodynamique suit la statistique de BoltzmannC.21 :
interagissant
avec des ions sous forme de particules aléatoirement distribuées. Le nuage électronique supposé en équilibre
thermodynamique suit la statistique de BoltzmannC.21 :
 |
(C.19) |
Cette statistique décrit le réarrangement des électrons en prèsence d'un potentiel
 qui leur permet de `` lutter '' contre
la force de répulsion coulombienne. Ainsi, dans le cas où le potentiel
qui leur permet de `` lutter '' contre
la force de répulsion coulombienne. Ainsi, dans le cas où le potentiel  augmente, l'influence de la répulsion
coulombienne diminue, donc la densité augmente jusqu'à équilibrer ces deux potentiels (
augmente, l'influence de la répulsion
coulombienne diminue, donc la densité augmente jusqu'à équilibrer ces deux potentiels ( et le potentiel d'interaction
entre électrons). Si la température augmente, les électrons acquièrent une énergie thermique supérieure, donc sous
l'effet de cette pression thermique, la densité diminue.
Ce potentiel
et le potentiel d'interaction
entre électrons). Si la température augmente, les électrons acquièrent une énergie thermique supérieure, donc sous
l'effet de cette pression thermique, la densité diminue.
Ce potentiel  peut ainsi être par exemple l'influence d'un
ion, qui perturbe l'uniformité de la densité de charge électronique. Cet ion nouvellement introduit force les électrons dans
une configuration différente, qui eux-mêmes en changeant leur disposition modifient le potentiel
peut ainsi être par exemple l'influence d'un
ion, qui perturbe l'uniformité de la densité de charge électronique. Cet ion nouvellement introduit force les électrons dans
une configuration différente, qui eux-mêmes en changeant leur disposition modifient le potentiel  . Il faut alors
introduire une équation supplémentaire, l'équation (C.1), appelée équation
de Poisson. Elle décrit le potentiel
créé par une certaine densité de charge : en
effet,
. Il faut alors
introduire une équation supplémentaire, l'équation (C.1), appelée équation
de Poisson. Elle décrit le potentiel
créé par une certaine densité de charge : en
effet,
 . Cet effet se
combine alors avec la statistique de Boltzmann.
. Cet effet se
combine alors avec la statistique de Boltzmann.

Étant donné que l'on considère un plasma globalement neutre (hypothèse de quasi neutralité) à l'équilibre,
on a
 ,
,  étant le degré moyen d'ionisation des ions. Ceci s'écrit aussi
étant le degré moyen d'ionisation des ions. Ceci s'écrit aussi
 . Si l'on considère que les ions sont immobiles, alors
. Si l'on considère que les ions sont immobiles, alors
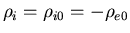 avec
avec  représentant la densité de charge électronique en l'absence de potentiel (à
représentant la densité de charge électronique en l'absence de potentiel (à  ), d'où
), d'où
 et
et  . Donc on a
. Donc on a
Dans l'hypothèse
 , c'est à dire dans l'hypothèse où la perturbation crée par un ion est
faible, on peut linéariser cette équation différentielle (développemente limité à l'ordre 1 :
, c'est à dire dans l'hypothèse où la perturbation crée par un ion est
faible, on peut linéariser cette équation différentielle (développemente limité à l'ordre 1 :  ) :
) :
Une solution de cette équation peut s'écrire (en 1D) sous la forme
 avec :
avec :
 |
(C.20) |
Cette grandeur 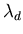 est la longueur de Debye, c'est la distance au bout de laquelle la perturbation dûe à la
prèsence de l'ion est écrantée par les électrons. On considérera donc que pour une distance inférieure à
est la longueur de Debye, c'est la distance au bout de laquelle la perturbation dûe à la
prèsence de l'ion est écrantée par les électrons. On considérera donc que pour une distance inférieure à 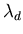 , le
potentiel vu est celui d'une charge nue, et que au delà, le potentiel n'est plus vu (écrantage). Lorsque les
dimensions considérées sont supérieures à la longueur de Debye, on peut modéliser le plasma par un ensemble d'ions se
déplaçant lentement et baignés par un fluide d'électronsC.22.
Une limitation de cette approche tient au nombre d'électrons présents dans la
sphère de DebyeC.23 afin que l'écrantage puisse vraiment avoir lieu ; il faut donc :
, le
potentiel vu est celui d'une charge nue, et que au delà, le potentiel n'est plus vu (écrantage). Lorsque les
dimensions considérées sont supérieures à la longueur de Debye, on peut modéliser le plasma par un ensemble d'ions se
déplaçant lentement et baignés par un fluide d'électronsC.22.
Une limitation de cette approche tient au nombre d'électrons présents dans la
sphère de DebyeC.23 afin que l'écrantage puisse vraiment avoir lieu ; il faut donc :
 |
(C.21) |
En règle générale, on considérera que l'écrantage peut avoir lieu si la particule se déplace moins vite que celles qui seraient responsables de cet écrantage. Ainsi, dans certains cas il peut être nécessaire de prendre en compte la contribution des ions. Il s'agit alors d'un écrantage de DEBYE-HÜCKELC.24.
Notes
- ...Boltzmann!statistiqueC.21
 étant la densité électronique,
étant la densité électronique,  le potentiel
électrostatique et
le potentiel
électrostatique et  la densité électronique quand
la densité électronique quand

- ... d'électronsC.22
- Dans le cas contraire, le comportement individuel des
électrons doit être pris en compte.
- ...Debye!sphèreC.23
- C'est la sphère de
rayon
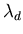 centrée sur l'ion
centrée sur l'ion
- ... Debye-HückelC.24
- Cet écrantage peut être retenu comme borne supérieure dans le logarithme coulombien, permettant le calcul d'une résistivité de DEBYE-HÜCKEL.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002


