C.4.9.1 Détermination d'une relation entre  et
et 
L'équation de l'énergie 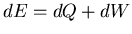 (voir (C.13)) s'écrit, si la propagation de la perturbation de densité
est adiabatiqueC.30 :
(voir (C.13)) s'écrit, si la propagation de la perturbation de densité
est adiabatiqueC.30 :
Or dans le cas d'un gaz parfait de 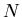 particules dans un volume
particules dans un volume  ,
,
Par définition,
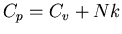 et
et
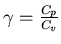 . Donc l'équation de l'énergie devient
. Donc l'équation de l'énergie devient
ce qui s'intègre en
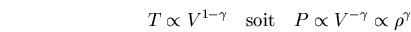 |
(C.26) |
Ceci signifie que
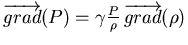
Notes
- ... adiabatiqueC.30
- Une onde sonore se propage suffisamment vite dans le milieu pour que les échanges d'énergie n'aient
pas le temps d'avoir lieu ; la compression/détente est alors adiabatique (
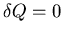 ,
,  étant la quantité de
chaleur).
étant la quantité de
chaleur).
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
