C.4.5.2 Onde électromagnétique transverse, fréquence de
coupure
Considérons le même plasma que précédemment, en faisant les mêmes hypothèses, mais en présence d'une onde électromagnétique.
Il faut alors ajouter deux équations décrivant les champs électromagnétiques :
En prenant le rotationnel de la première équation et la dérivée de la seconde, si l'on considère que
 ,
alors puisque
,
alors puisque
 on a :
on a :
En faisant une modélisation en onde plane, c'est à dire si l'on a une dépendance en
 (dans le cas 1D,
voir section C.4.8 pour un développement plus complet), alors ceci s'écrit :
(dans le cas 1D,
voir section C.4.8 pour un développement plus complet), alors ceci s'écrit :
car l'onde que l'on cherche est transverse, ce qui implique
 .
De plus, on fait l'hypothèse que le courant est électronique, donc
.
De plus, on fait l'hypothèse que le courant est électronique, donc
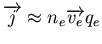 . D'après l'équation
du mouvement linéarisée pour les électrons et en dépendance exponentielle (voir section C.4.5.1),
. D'après l'équation
du mouvement linéarisée pour les électrons et en dépendance exponentielle (voir section C.4.5.1),
 . La relation de dispersion s'écrit ainsi (avec
. La relation de dispersion s'écrit ainsi (avec
 et
et
 la fréquence plasma des électrons)
la fréquence plasma des électrons)
 |
(C.18) |
Si la fréquence de l'onde électromagnétique est supérieure à la fréquence plasma, alors le vecteur d'onde  est réel,
l'onde se propage dans le plasma. Dans le cas contraire, le vecteur d'onde est imaginaire, donc on assiste à un
amortissement exponentiel. La fréquence plasma agit donc comme une fréquence de coupure.
Physiquement, cela signifie que lorsque la fréquence de l'onde est suffisamment faible, le plasma a le temps de réagir et de
se réorganiser de façon à neutraliser la perturbation.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
est réel,
l'onde se propage dans le plasma. Dans le cas contraire, le vecteur d'onde est imaginaire, donc on assiste à un
amortissement exponentiel. La fréquence plasma agit donc comme une fréquence de coupure.
Physiquement, cela signifie que lorsque la fréquence de l'onde est suffisamment faible, le plasma a le temps de réagir et de
se réorganiser de façon à neutraliser la perturbation.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002

 ,
alors puisque
,
alors puisque
