Afin de vérifier la validité des approximations réalisées
dans le cas d'un liner de compression de flux, une simulation 1D
a été
réalisée avec Mach2
.
Figure 2.20:
configuration de la simulation de diffusion au travers du liner: nombre
de cellules du maillage en fonction du rayon
|
|
Cette simulation comprend une tranche de plasma
d'aluminium soumise à un courant typique de ce qui est injecté sur Z
pour nos
liners de compression de flux. Afin de simplifier le problème, aucun courant
secondaire n'est injecté, mais par contre un champ magnétique stabilisateur 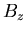 est
appliqué. Sa valeur initiale dans le plasma est faible, afin de prendre en compte
l'établissement de ce champ dans un fil initialement froid suivit de l'explosion
rapide de ce fil pour former une coquille de plasma.
La coquille est maillée avec 200 mailles lagrangiennes, le pseudo-vide compris entre
le barreau central en comprenant 72. Un modèle de résistivité dérivé du modèle de
Spitzer
est utilisé et des équations d'état issues de Sesame
sont
employées pour le liner. La simulation n'utilise que deux seuils sur les densités:
est
appliqué. Sa valeur initiale dans le plasma est faible, afin de prendre en compte
l'établissement de ce champ dans un fil initialement froid suivit de l'explosion
rapide de ce fil pour former une coquille de plasma.
La coquille est maillée avec 200 mailles lagrangiennes, le pseudo-vide compris entre
le barreau central en comprenant 72. Un modèle de résistivité dérivé du modèle de
Spitzer
est utilisé et des équations d'état issues de Sesame
sont
employées pour le liner. La simulation n'utilise que deux seuils sur les densités:
- un seuil général à
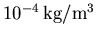 ;
;
- un seuil sur l'effet JOULE à
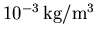 ;
;
Cette configuration est présentée en figure 2.20.
Figure:
simulation de diffusion au travers du liner: double épaisseur de peau sur
les profils de densité et de champs magnétiques
|
|
Conformément aux calculs présentés, les résultats de la simulation de la figure
2.21 mettent en évidence deux profils en exponentielle ainsi que
deux épaisseurs de peau, pour la densité (
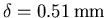 ) et pour le champ
magnétique (
) et pour le champ
magnétique (
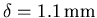 , soit effectivement le double de celle de la densité).
Il est d'ailleurs intéressant de noter que quelque
soit le profil initial de densité, le calcul converge vers ce profil
expontentiel1.16. Les oscillations visibles sur la
courbe de densité au voisinage du passage dans le vide viennent de conditions de
densité et de températures tellement hors du régime cinétique que le modèle de
SPITZER diverge (voir en
section D.6.3 page
, soit effectivement le double de celle de la densité).
Il est d'ailleurs intéressant de noter que quelque
soit le profil initial de densité, le calcul converge vers ce profil
expontentiel1.16. Les oscillations visibles sur la
courbe de densité au voisinage du passage dans le vide viennent de conditions de
densité et de températures tellement hors du régime cinétique que le modèle de
SPITZER diverge (voir en
section D.6.3 page ![[*]](./icons/crossref.png) ). On
remarquera aussi le
front de choc lissé par la viscosité numérique (lissage sur 4 cellules paramétré dans
la namelist). Ceci est dû au pseudo-vide: la densité étant faible, la vitesse sonore
est trop faible pour éviter la formation d'un choc à l'avant (face interne) du liner.
Avec un vide réel, la densité serait tellement faible que le choc ne se formerait pas
faute de matière contre laquelle entrer en collision. Cet effet purement numérique
doit donc se voir dans toutes les simulations utilisant un
pseudo-vide.
). On
remarquera aussi le
front de choc lissé par la viscosité numérique (lissage sur 4 cellules paramétré dans
la namelist). Ceci est dû au pseudo-vide: la densité étant faible, la vitesse sonore
est trop faible pour éviter la formation d'un choc à l'avant (face interne) du liner.
Avec un vide réel, la densité serait tellement faible que le choc ne se formerait pas
faute de matière contre laquelle entrer en collision. Cet effet purement numérique
doit donc se voir dans toutes les simulations utilisant un
pseudo-vide.
Notes
- ...
expontentiel1.16
- Le seule différence, du point de vue de la simulation réside
alors dans le temps de calcul: une simulation initialisée avec un profil en
exponentiel sera caractérisée par un pas de temps quasi constant, alors que dans le
cas contraire, le pas de temps sera très faible avant de croître au fur et à mesure
que le profil se rapproche du profil expontentiel.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
![\rotatebox{-90}{\includegraphics[height=\textwidth]{figures/liner_results_cells.ps}}](img300.png)
![\rotatebox{0}{\includegraphics[width=\textwidth]{figures/liner_results_mag.ps}}](img303.png)