1.4.1.2 Influence du précurseur sur Z
Le générateur Z
offre la possibilité d'utiliser plusieurs
`` modes '' pour les courants
primaire et secondaire: le mode court (
 de temps de monté), le mode
normal (
de temps de monté), le mode
normal (
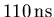 ) et le mode long (
) et le mode long (
 ).
Lorsque le générateur secondaire est en
mode court alors que le générateur primaire est en mode long (cas du tir
Z780
), le précurseur a le temps de remplir la cavité secondaire. Le
générateur secondaire doit donc injecter son flux dans un milieu empli de plasma
basse densité. Il peut donc se former une sorte de `` poche de flux '', c'est à dire
un espace dans lequel un certain flux magnétique a été établi et pour lequel la
densité est plus faible que dans le reste de la cavité secondaire. En effet, la
pression magnétique du secondaire chasse le plasma précurseur.
Il est possible d'estimer la densité de plasma précurseur présente dans l'espace
compris entre le liner et le barreau central: considérons qu'une masse
).
Lorsque le générateur secondaire est en
mode court alors que le générateur primaire est en mode long (cas du tir
Z780
), le précurseur a le temps de remplir la cavité secondaire. Le
générateur secondaire doit donc injecter son flux dans un milieu empli de plasma
basse densité. Il peut donc se former une sorte de `` poche de flux '', c'est à dire
un espace dans lequel un certain flux magnétique a été établi et pour lequel la
densité est plus faible que dans le reste de la cavité secondaire. En effet, la
pression magnétique du secondaire chasse le plasma précurseur.
Il est possible d'estimer la densité de plasma précurseur présente dans l'espace
compris entre le liner et le barreau central: considérons qu'une masse  issue de
l'explosion des fils est émise de façon régulière pendant un temps
issue de
l'explosion des fils est émise de façon régulière pendant un temps  . La matière
doit parcourir une distance
. La matière
doit parcourir une distance 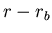 à une vitesse constante
à une vitesse constante  , qui correspond à sa
vitesse d'émission. Si le liner est de hauteur
, qui correspond à sa
vitesse d'émission. Si le liner est de hauteur  , alors il y a une densité
, alors il y a une densité  dans la zone secondaire qui vaut:
dans la zone secondaire qui vaut:
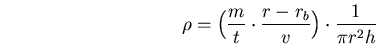
Ainsi, pour le tir Z780
, si l'on estime que la vitesse d'expansion du plasma
issu des fils est de
 (voir
en annexe, table G.1 page
(voir
en annexe, table G.1 page ![[*]](./icons/crossref.png) ), que le rayon du
liner de
), que le rayon du
liner de
 de haut est
de haut est
 avec un rayon moyen de barreau de
avec un rayon moyen de barreau de
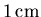 et que
et que 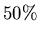 de la masse du liner est émise en
de la masse du liner est émise en  du temps
d'implosion (voir en annexe G.3 page
du temps
d'implosion (voir en annexe G.3 page ![[*]](./icons/crossref.png) ),
alors la densité du précurseur devrait être de
),
alors la densité du précurseur devrait être de
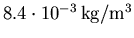 .
La figure 2.15 présente les contours d'iso-densité
simulés en MHD
2D
pour le tir Z780
, avec un précurseur de densité
.
La figure 2.15 présente les contours d'iso-densité
simulés en MHD
2D
pour le tir Z780
, avec un précurseur de densité
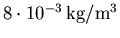 , ainsi que les contours de densité de courant sur la
figure 2.16.
, ainsi que les contours de densité de courant sur la
figure 2.16.
Figure:
poche de flux: densité de matière
![\rotatebox{90}{\includegraphics[height=\textwidth]{figures/poche_rho.ps}}](img239.png)
|
Figure:
poche de flux: densité de courant
![\rotatebox{90}{\includegraphics[height=\textwidth]{figures/poche_j.ps}}](img240.png)
|
Cette simulation est en fait une simulation habituelle de la compression de flux sur
Z
, mais pour laquelle le courant secondaire est injecté via une condition aux
limites sur le fond d'un petit gap (en bas sur le tracé de la densité de courant) et
l'espace secondaire est empli d'une densité initiale telle que cela représente la
moitié de la masse du liner.
La poche de flux est bien visible, matérialisée par une densité plus faible que le
précurseur initial, et coincée entre le liner et le barreau central. Le plasma
précuseur qui a été chassé de la poche s'accumule sur le bord de cette poche (effet
chasse-neige), et le liner en avançant aide celle-ci à migrer vers un rayon plus
petit. En effet, la pression magnétique augmentant lorsque le rayon diminue, les
parties de cette poche qui se situent au plus petit rayon sont celles qui poussent le
plus sur ce qui délimite la poche. Donc la partie supérieure de la poche progresse
en chassant le précurseur, tandis que le liner écrase la partie inférieure de la
poche, pour laquelle la pression magnétique est plus faible. Il ne faut par contre
pas s'imaginer que le flux magnétique chasse la totalité de la matière en
s'installant: le nombre de Reynolds magnétique du plasma précurseur étant
voisin de un, l'effet diffusif est aussi important que l'effet convectif, donc tandis
qu'une partie de la matière est chassée vers l'extèrieur (convection), l'autre partie
est insensible au champ magnétique (diffusion résistive).
La courbe d'iso densité de courant (figure 2.16) met en évidence
le circuit primaire (boucle de courant la
plus à droite), le circuit du générateur secondaire (boucle de courant du
milieu) et le circuit du secondaire amplifié (boucle de courant à gauche). Le code
n'a pas été capable de gérer correctement le bouchage du gap d'injection par le
plasma1.13, ce qui explique que le générateur secondaire
parvienne encore à injecter du courant dans le liner, le faisant `` exploser '' à sa
base.
Notes
- ... simulé1.13
- En effet, le bouchage d'un tel gap par un plasma échappe à la
modélisation MHD
habituelle (faibles densités, rupture possible de la
quasi-neutralité électrique ...) ainsi qu'à la modélisation PIC
de par la
trop grande densité du plasma.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002