H.3.2 Influence de la diffusivité du pseudo vide
Étant donné que la diffusivité du pseudo vide est en général un paramètre libre des
codes MHD
, c'est à dire un paramètre
que l'on impose dans la namelist du code, on aurait tendance à vouloir la fixer à une grande valeur. Ceci peut sembler
logique, en fixant une grande vitesse de diffusion dans les zones contenant du pseudo vide, et sans risques. Or, ce
paramètre est en fait beaucoup moins indépendant qu'il n'y parait, comme nous allons le voir.
Tout d'abord, afin de résoudre correctement la diffusion des champs, c'est à dire que la diffusion
numérique soit bien plus
faible que la diffusion physique, il faut respecter :
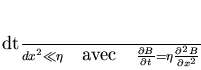 |
(H.4) |
En fait, d'une manière plus générale, 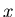 représente les directions spatiales. Ceci signifie que pour un échantillonnage
spatial et temporel donné, il est possible d'améliorer le calcul de la diffusion des champs dans un milieu (donc dans
le vide) en jouant sur l'échantillonnage spatial et temporel ou bien sur sa diffusivité.
Mais la diffusivité joue aussi sur les champs électriques :
représente les directions spatiales. Ceci signifie que pour un échantillonnage
spatial et temporel donné, il est possible d'améliorer le calcul de la diffusion des champs dans un milieu (donc dans
le vide) en jouant sur l'échantillonnage spatial et temporel ou bien sur sa diffusivité.
Mais la diffusivité joue aussi sur les champs électriques :
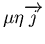 représente un champ électrique.
Or d'après
représente un champ électrique.
Or d'après
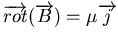 , une erreur sur le calcul de
, une erreur sur le calcul de
 (de par la précision
limitée de la machine, du code ou bien lorque le critère (H.4) n'est
pas respecté) se traduit par la création d'un courant, qui lui même crée une tension.
Imaginons que l'on se donne un
(de par la précision
limitée de la machine, du code ou bien lorque le critère (H.4) n'est
pas respecté) se traduit par la création d'un courant, qui lui même crée une tension.
Imaginons que l'on se donne un 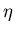 très grand : dans ce cas, la diffusion devrait être très bien traitée, la diffusion
numérique étant très faible devant la diffusion physique. Mais le code (ou la machine)
fait les calculs à une précision
numérique limitée, du fait de la représentation des nombres par une suite finie de bytes. Ceci signifie donc que malgré des
conditions à priori favorables, le code ne parvient pas à créer un
très grand : dans ce cas, la diffusion devrait être très bien traitée, la diffusion
numérique étant très faible devant la diffusion physique. Mais le code (ou la machine)
fait les calculs à une précision
numérique limitée, du fait de la représentation des nombres par une suite finie de bytes. Ceci signifie donc que malgré des
conditions à priori favorables, le code ne parvient pas à créer un
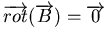 . Ceci est un petit
. Ceci est un petit
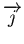 qui va ensuite être multiplié par
qui va ensuite être multiplié par 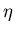 , et ceci crée un champ électrique qui peut devenir énorme, c'est à
dire très grand devant le champ électrique physique.
Ce qu'il faut retenir, c'est que en se fixant un
, et ceci crée un champ électrique qui peut devenir énorme, c'est à
dire très grand devant le champ électrique physique.
Ce qu'il faut retenir, c'est que en se fixant un 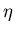 donné, on s'impose une précision minimum à atteindre sur le calcul
des champs. Si le code n'est pas capable de travailler à cette précision, la simulation sera fausse alors que le pseudo vide
que l'on s'est donné semble bon. Il vaut mieux alors conserver un
donné, on s'impose une précision minimum à atteindre sur le calcul
des champs. Si le code n'est pas capable de travailler à cette précision, la simulation sera fausse alors que le pseudo vide
que l'on s'est donné semble bon. Il vaut mieux alors conserver un 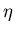 raisonnable, et plutôt jouer sur l'échantillonnage -- via le facteur
raisonnable, et plutôt jouer sur l'échantillonnage -- via le facteur
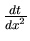 -- pour diminuer la diffusion numérique.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
-- pour diminuer la diffusion numérique.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002