F.1.1.2 Paramètres de la simulation
Figure F.1:
maillage de la simulation d'explosion de conducteur
|
|
Cette simulation, dont le maillage est présenté en figure F.1,
à été réalisée avec Mach2
et se compose de deux blocs de matériaux distincts :
- bloc 1
- constitué d'un gaz parfait de densité
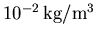 ,
de degré d'ionisation
,
de degré d'ionisation 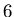 et de
résistivité constante à
et de
résistivité constante à
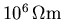 . Ceci modélise le vide qui se trouve entre le
retour de courant et le barreau central, et le choix des modèles physique trouve
sa justification dans le régime plasma d'un tel vide : à basse densité, un
plasma atteint le régime cinétique même pour des températures relativement peu
élevées. Par contre, du fait de la densité anormalement élevée pour du
videF.2, il est
nécessaire d'imposer une résistivité constante au lieu d'utiliser un modèle de
SPITZER, qui bien que physiquement justifié, aurait conduit à une
diffusivité trop faible. Pour la même raison, il est nécessaire d'interdire le
chauffage joule et la résolution de l'hydrodynamique dans ce bloc.
. Ceci modélise le vide qui se trouve entre le
retour de courant et le barreau central, et le choix des modèles physique trouve
sa justification dans le régime plasma d'un tel vide : à basse densité, un
plasma atteint le régime cinétique même pour des températures relativement peu
élevées. Par contre, du fait de la densité anormalement élevée pour du
videF.2, il est
nécessaire d'imposer une résistivité constante au lieu d'utiliser un modèle de
SPITZER, qui bien que physiquement justifié, aurait conduit à une
diffusivité trop faible. Pour la même raison, il est nécessaire d'interdire le
chauffage joule et la résolution de l'hydrodynamique dans ce bloc.
- bloc 2
- constitué de cuivre à la densité solide, dont les équations
d'états proviennent de SESAME
, de même que la résitivité. Ce bloc ne comporte
aucun seuil de densité limitant certains phénomènes physiques, excepté le seuil
de densité globale fixé pour les deux blocs à
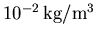 .
.
Ces deux blocs sont lagrangiens, seul le coté gauche du bloc 1 reste à une abscisse
fixe car c'est par cette limite que le courant électrique est injecté, via une
condition aux limites sur le champ magnétique. Le premier bloc comporte 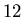 mailles
sur une longueur de
mailles
sur une longueur de
 , tandis que le second compte
, tandis que le second compte  mailles pour
mailles pour
 , avec un maillage quadratique permettant d'utiliser des mailles de
, avec un maillage quadratique permettant d'utiliser des mailles de
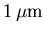 sur la face interne.
sur la face interne.
Les conditions aux limites retenues répondent à deux critères : permettre une
résolution la plus proche possible d'un cas 1D
, et la plus fidèle possible à
l'expérience. C'est pourquoi le champ magnétique imposé sur le coté gauche du bloc 1
est calculé à partir du courant simulé pour le tir Z635, et les conditions aux limites
sur les bords hauts et bas des blocs sont des conditions de symétrie pour le champ
magnétique et la pression ; et une condition de rayonnement de corps noir afin d'être
proche du modèle de rayonnement en volume appliqué à l'intérieur des
cellulesF.3. Enfin, le maillage a été choisit de façon à pouvoir
résoudre suffisament bien les épaisseurs de peau qui nous intéressent (de l'ordre de
la dizaine de microns pour une limite basse). Le maillage dépend aussi de la
viscosité numérique que l'on utilise: un lissage des chocs sur  cellules signifie
que les phénomènes hydrodynamiques d'échelle inférieure à
cellules signifie
que les phénomènes hydrodynamiques d'échelle inférieure à  cellules ne peuvent pas
prétendre être traités. Les mailles dans le pseudo-vide doivent quant à elles
simplement permettre une véritable diffusion du champ magnétique. C'est pourquoi une
diffusivité de
cellules ne peuvent pas
prétendre être traités. Les mailles dans le pseudo-vide doivent quant à elles
simplement permettre une véritable diffusion du champ magnétique. C'est pourquoi une
diffusivité de 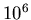 a été retenue (valeur acceptable en terme de capacité à
résoudre la diffusion magnétique pour le code) et une taille de maille inférieure à
a été retenue (valeur acceptable en terme de capacité à
résoudre la diffusion magnétique pour le code) et une taille de maille inférieure à
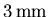 (pour que la diffusion soit d'origine physique et non pas numérique tout
en utilisant un pas de temps raisonnable)F.4.
(pour que la diffusion soit d'origine physique et non pas numérique tout
en utilisant un pas de temps raisonnable)F.4.
Notes
- ... videF.2
- Ceci provient du fait que Mach2
tolère mal de trop grandes
plages de densité
- ...
cellulesF.3
- Ce modèle de rayonnement conduit à sur-estimer les pertes, donc la
température calculée dans la simulation est une valeur minimale. Enfin, ces
conditions aux limites sont redondantes avec le modèle utilisé dans l'intérieur du
maillage, mais ceci doit permettre ensuite d'utiliser les mêmes paramètres dans des
simulations 2D
.
- ... raisonnable)F.4
- Pour les explications détaillées
sur les concepts exploités ici, voir
section H.1.7 page
![[*]](./icons/crossref.png) et section H.3.2 page
et section H.3.2 page ![[*]](./icons/crossref.png)
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
![]() cellules signifie
que les phénomènes hydrodynamiques d'échelle inférieure à
cellules signifie
que les phénomènes hydrodynamiques d'échelle inférieure à ![]() cellules ne peuvent pas
prétendre être traités. Les mailles dans le pseudo-vide doivent quant à elles
simplement permettre une véritable diffusion du champ magnétique. C'est pourquoi une
diffusivité de
cellules ne peuvent pas
prétendre être traités. Les mailles dans le pseudo-vide doivent quant à elles
simplement permettre une véritable diffusion du champ magnétique. C'est pourquoi une
diffusivité de ![]() a été retenue (valeur acceptable en terme de capacité à
résoudre la diffusion magnétique pour le code) et une taille de maille inférieure à
a été retenue (valeur acceptable en terme de capacité à
résoudre la diffusion magnétique pour le code) et une taille de maille inférieure à
![]() (pour que la diffusion soit d'origine physique et non pas numérique tout
en utilisant un pas de temps raisonnable)F.4.
(pour que la diffusion soit d'origine physique et non pas numérique tout
en utilisant un pas de temps raisonnable)F.4.