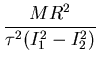1.3.1.4 Dynamique du liner
Le liner de masse  et de hauteur
et de hauteur  est soumis aux forces de LAPLACE
(
est soumis aux forces de LAPLACE
(
 ) du fait du courant primaire
) du fait du courant primaire  qui l'implose et via le
courant secondaire
qui l'implose et via le
courant secondaire  qui s'oppose à cette implosion. D'après le premier principe de la dynamique (
qui s'oppose à cette implosion. D'après le premier principe de la dynamique (
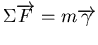 ), et l'expression de la force magnétique sur un conducteur parcouru par un courant:
), et l'expression de la force magnétique sur un conducteur parcouru par un courant:
Considérons les unités normalisées suivantes:
Nous avons alors:
Les solutions de l'équation de la dynamique du liner ne dépendent plus que du
paramètre  . Ce paramètre définit alors en quelque sorte des classes de
problèmes, pour lesquels exactement la même équation est résolue (en
effet, tous les autres paramètres intervenant dans l'équation sont
adimensionés), donc pour lesquels les solutions sont les mêmes (même
. Ce paramètre définit alors en quelque sorte des classes de
problèmes, pour lesquels exactement la même équation est résolue (en
effet, tous les autres paramètres intervenant dans l'équation sont
adimensionés), donc pour lesquels les solutions sont les mêmes (même
 ).
Le paramètre sans dimension
).
Le paramètre sans dimension  est caractéristique de la dynamique du liner de
plasma. Deux expériences de même
est caractéristique de la dynamique du liner de
plasma. Deux expériences de même  à tout instant1.9 auront donc la même dynamique, donc le même temps d'impact
sur le barreau central, et la même énergie du fait d'un couplage avec les générateurs primaires et secondaires
identiques.
Ce prérequis de même profil temporel n'est évidement pas tenable pour la
compression de flux, donc on peut utiliser comme courant
à tout instant1.9 auront donc la même dynamique, donc le même temps d'impact
sur le barreau central, et la même énergie du fait d'un couplage avec les générateurs primaires et secondaires
identiques.
Ce prérequis de même profil temporel n'est évidement pas tenable pour la
compression de flux, donc on peut utiliser comme courant  l'amplitude du courant
secondaire injecté et comme courant
l'amplitude du courant
secondaire injecté et comme courant  l'amplitude du courant primaire. Ceci
permet de réaliser une petite correction sur la dynamique du liner par rapport à une
dynamique de pinch (pour lequel le raisonnement présenté dans ce paragraphe est
habituellement utilisé) en prenant en
compte la présence du secondaire1.10.
l'amplitude du courant primaire. Ceci
permet de réaliser une petite correction sur la dynamique du liner par rapport à une
dynamique de pinch (pour lequel le raisonnement présenté dans ce paragraphe est
habituellement utilisé) en prenant en
compte la présence du secondaire1.10.
Notes
- ... instant1.9
- Et de même profil de courant temporel
- ... secondaire1.10
- De toute façon, le secondaire amplifié
n'intervient que brièvement et à la toute fin, donc la majeur partie de la dynamique
aura lieu à une valeur de courant secondaire proche du courant secondaire injecté.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002