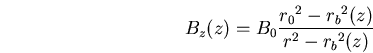1.3.1.5 Compression de 
Un champ magnétique  , appelé champ stabilisateur est parfois utilisé pour
modérer le développement des instabilités (voir section 2.3.3.3 page
, appelé champ stabilisateur est parfois utilisé pour
modérer le développement des instabilités (voir section 2.3.3.3 page ![[*]](./icons/crossref.png) ). La
compression d'un tel champ ne suit pas la même dynamique que celle du champ
). La
compression d'un tel champ ne suit pas la même dynamique que celle du champ
 .
Nous allons traiter le cas de la compression de
.
Nous allons traiter le cas de la compression de  par un liner contre un barreau central de rayon
par un liner contre un barreau central de rayon
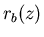 connu, en faisant
l'approximation
connu, en faisant
l'approximation
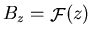 (donc
(donc 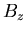 uniforme selon
uniforme selon  ) à l'intérieur du volume délimité par le liner. Nous avons donc:
) à l'intérieur du volume délimité par le liner. Nous avons donc:
Ici,  représente le rayon du liner au moment où le flux de
représente le rayon du liner au moment où le flux de 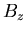 se fait piéger, c'est à dire au moment de la
formation de la coquille (qui permet alors l'existence du courant
se fait piéger, c'est à dire au moment de la
formation de la coquille (qui permet alors l'existence du courant 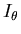 ).
Il est alors possible d'en déduire le champ magnétique
).
Il est alors possible d'en déduire le champ magnétique 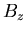 à tout instant à une hauteur
à tout instant à une hauteur  :
:
Ceci signifie que l'énergie magnétique contenue dans une tranche de hauteur 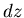 , le rayon du liner étant
, le rayon du liner étant  est :
est :
Il est donc possible de calculer le coût énergétique de la compression de 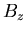 à un rayon donné, connaissant le
rayon du barreau en fonction de
à un rayon donné, connaissant le
rayon du barreau en fonction de  ,
,
 :
:
L'énergie que l'on va consommer pour compresser le flux de 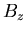 d'un rayon
d'un rayon  à un rayon
à un rayon  est donc:
est donc:
Dans le cas d'un barreau cylindrique de rayon
 , la compression de
, la compression de 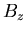 consomme alors
consomme alors
Dans un cas de compression de flux classique (dimensions de z591
), avec un courant secondaire au moment du crowbar de
 , à un rayon
, à un rayon
 avec une hauteur de liner de
avec une hauteur de liner de
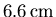 , et un
, et un
 , l'énergie consommée
par la compression du
, l'énergie consommée
par la compression du  reste toujours très largement supérieure à celle consommée par la compression du
reste toujours très largement supérieure à celle consommée par la compression du
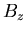 (courbe 2.9).
(courbe 2.9).
Figure:
comparaison des énergies magnétiques contenues dans les champs  et
et 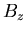 lors de la compression de flux sur Z
, en fonction du rayon du
liner
lors de la compression de flux sur Z
, en fonction du rayon du
liner
|
|
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002