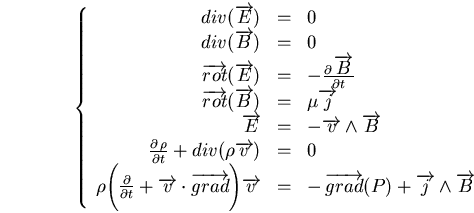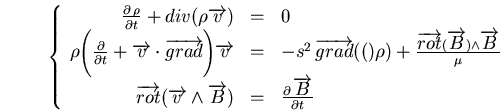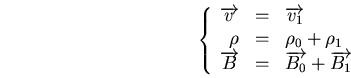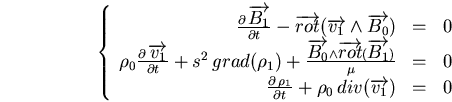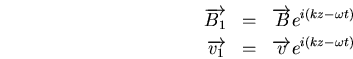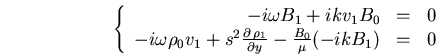C.4.8 Vitesse d'ALFVÉN
Considérons un plasma comme un fluide non visqueux, compressible et conducteur idéal plongé dans un champ magnétique
uniforme
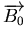 . Les équations décrivant ceci sont :
. Les équations décrivant ceci sont :
Ce qui, pour un gaz parfait se ramène àC.29 :
En linéarisant ceci au premier ordre sous la forme de petites perturbations autour d'un état d'équilibre, avec :
On obtient alors :
On cherche alors une solution de ce système sous la forme d'onde plane, telle que
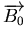 et
et
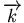 soient dirigés
selon l'axe
soient dirigés
selon l'axe
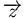 , et que
, et que
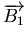 et
et
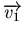 (c'est à dire la perturbation) soient dirigés selon l'axe
(c'est à dire la perturbation) soient dirigés selon l'axe
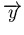 (voir figure C.6). On suppose donc que
(voir figure C.6). On suppose donc que
On obtient alors le système suivant (projeté sur l'axe
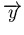 ) :
) :
Ceci décrit donc une onde se propageant parallèlement à
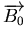 de vitesse de phase (
de vitesse de phase (
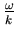 ) :
) :
 |
(C.25) |
Cette onde est une onde plane (pas de variation spatiale de la densité autre que dans la direction de la perturbation)
magnétohydrodynamique (elle existe de part la
présence d'un champ magnétique et grâce aux propriétés hydrodynamiques du plasma) ;
c'est l'onde d'Alfvén. On peut
s'imaginer les lignes de forces magnétiques comme les cordes d'une guitare, et l'onde
d'Alfvén comme l'onde que crée le
musicien en écartant transversalement la corde de sa position d'équilibre.
Cette onde rend possible la propagation d'un champ magnétique dans un matériau
conducteur, quelle que soit sa conductivité. Un champ magnétique peut donc soit
diffuser, en étant alors fortement atténué dans le cas d'un milieu peu diffusif, soit
se propager par une onde d'Alfvén, qui lui permet d'être peu atténué ; ce mode
de propagation n'étant rendu possible que par le couplage entre la matière et le champ
magnétique.
Notes
- ... àC.29
- On rappelle que l'équation d'état d'un gaz parfait s'écrit
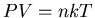 (
( étant le nombre de particules présentes) ; c'est à dire que pour une masse de gaz
étant le nombre de particules présentes) ; c'est à dire que pour une masse de gaz 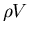 de particules de masse
de particules de masse
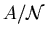 (
(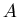 étant la masse atomique de l'élément considéré et
étant la masse atomique de l'élément considéré et 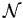 le nombre d'Avogadro) l'équation d'état
s'écrit
le nombre d'Avogadro) l'équation d'état
s'écrit 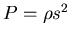 avec
avec
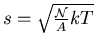 une vitesse
thermique des particules composant le gaz.
une vitesse
thermique des particules composant le gaz.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002