C.4.5.1 Ondes de LANGMUIR

Supposons un plasma globalement neutre, dont on va `` extraire `` une lame d'électrons^C.20. Le plasma est maintenant composé d'une partie chargée positivement (car elle contient un excès d'ions) et d'une partie chargée négativement (les électrons que l'on a écartés du reste du plasma). Si l'on relache alors les électrons, ils vont être accélérés sous l'effet de la charge d'espace (création d'un champ électrique), vont atteindre leur position d'équilibre (permettant au champ électrique d'être nul) et atteindre une vitesse nulle pour une position comportant un excès d'électrons (voir figure C.5)

Figure C.5: oscillations plasma

Le fait d'avoir écarté les électrons de leur position d'équilibre produit donc des oscillations. Afin de calculer la fréquence de ces oscillations, on fait les hypothèses suivantes :

• ions immobiles (du fait de leur grande masse devant celle des électrons) ;
• fluide électronique (pas de comportement particulaire individuel, voir section C.4.6) ;
• pas de champs électromagnétiques externes ;
• agitation thermique négligeable, donc $\mathop{\overrightarrow{grad}}({P_e}) \approx 0$ ;
• collisions négligeables, donc pas de terme de viscosité.

Les équations décrivant alors le système sont les équations de conservation de la masse, l'équation de Poisson (création d'un champ électrique par une densité de charge) et le premier principe de la dynamique pour des électrons qui ne sont plus soumis qu'à une force électrique :

$$\left\{ \begin{array}{rcl} \frac{\partial \, {n_e}}{\p... ..._e} & = & n_e q_e \overrightarrow{E} \end{array} \right.$$

On fait l'hypothèse que les oscillations sont de faible amplitude, ce qui permet de linéariser (développement de limité d'ordre 1) le système d'équations avec

$$\left\{ \begin{array}{rcl} n_e & = & n_{e0} + \tilde{n... ...e} \quad \mbox{avec } v_0 \approx 0 \end{array} \right.$$

en faisant l'hypothèse de la quasi neutralité électrique et de petits déplacements autour d'un état d'équilibre. En ne gardant que les termes d'ordre 1, le système devient :

$$\left\{ \begin{array}{rcl} \frac{\partial \, {\tilde{n... ... & q_e \overrightarrow{\tilde{E_e}} \end{array} \right.$$

En admettant que $\mathop{div}({\frac{\partial \, {\overrightarrow{\tilde{v_e}}}}{\partial {t}}}) = \frac{\partial \, {\mathop{div}(\overrightarrow{{\tilde{v_e}}})}}{\partial {t}}$, alors on obtient l'équation différentielle

$$\frac{\partial^2 \, \tilde{n_e}}{\partial t^2} = \frac{n_{e0} {q_e}^2}{\varepsilon m_e} \tilde{n_e}$$

dont les solutions sont de la forme 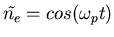$\tilde{n_e} = \mathop{cos}(\omega_p t)$ avec

$$\omega_p = \sqrt{\frac{n_{e0} {q_e}^2}{\varepsilon m_e}}$$ (C.16)

Cette pulsation dépend donc de la masse de l'électron, de sa charge et de la densité électronique moyenne. Il est possible de définir de la même façon une fréquence plasma ionique (en fait, c'est une pulsation)

$$\Omega_p = \sqrt{\frac{n_{i0} {q_i}^2}{\varepsilon m_i}}$$ (C.17)

qui est bien plus faible que celle des électrons. On définit aussi la pulsation

$$\omega_0 = \sqrt{{\omega_p}^2 + {\Omega_p}^2}$$

qui en pratique est très voisine de celle des électrons. Dans un plasma classique (donc ayant un grand nombre d'électrons dans la sphère de Debye), la fréquence plasma est plus grande que n'importe quelle fréquence de collision.

Notes

... d'électrons^C.20

À l'aide d'un champ électrique par exemple