C.1.1.3 Le rotationnel
Figure:
opérateur rotationnel
|
|
On note
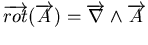 , l'opérateur rotationnel. Si
, l'opérateur rotationnel. Si 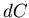 représente
la circulation
du vecteur
représente
la circulation
du vecteur
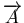 le long d'un contour
le long d'un contour  délimitant une surface
délimitant une surface  , on a (voir figure C.2) :
, on a (voir figure C.2) :
Le flux du rotationnel d'un vecteur
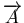 à travers une surface
à travers une surface  représente donc
la circulation de celui-ci le long du
contour délimitant cette surface. Une grandeur ayant un rotationnel nul, telle que
représente donc
la circulation de celui-ci le long du
contour délimitant cette surface. Une grandeur ayant un rotationnel nul, telle que
 dans le cas où il n'y a pas de
variations de l'induction a donc une circulation nulle sur un contour (
dans le cas où il n'y a pas de
variations de l'induction a donc une circulation nulle sur un contour (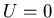 dans ce cas).
dans ce cas).
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002