3.1.2 Tirs de hautes pressions

La seconde catégorie de tirs réalisés lors de ce programme expérimental concerne l'étude des matériaux sous contrainte. Ceci consiste à appliquer une contrainte connue (pression) sur un échantillon puis à étudier l'état du matériau $(P,V,\rho)$. On se propose alors d'utiliser le champ magnétique pour générer une pression à la surface d'un échantillon (pression magnétique). Le gradient de pression magnétique est défini par

$$\frac{d \, P}{dx} = - \mu H \frac{\partial \, H}{\partial x}$$

Si l'échantillon est très épais devant l'épaisseur de peau de la diffusion du champ magnétique^3.2 -- c'est à dire si le champ magnétique est maximal d'un côté de l'échantillon et nul de l'autre -- la pression vue sera (en fonction du champ magnétique appliqué à la surface de l'échantillon):

$$\index{équation!pression magnétique} P_{magn\acute{e}tique} = \frac{B^2}{2 \mu}$$

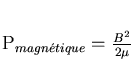
On construit alors une charge (qui n'est qu'une inductance morte, du point de vue du générateur) sur laquelle prend place un échantillon. Plusieurs géométries sont possibles, notamment la géométrie cylindrique (les anodes et cathodes sont deux cylindres coaxiaux), la géométrie ligne plate (anode et cathode se font face) et la géométrie charge carrée (qui pourrait se définir comme une charge coaxiale de section carrée). Ces différentes charges sont illustrées sur la figure 4.1.

Figure: hautes pressions: charge cylindrique, ligne plate, charge carrée

Pour une charge coaxiale, l'échantillon peut alors être placé sur le barreau central de la charge (voir [12]), ou bien sur son retour de courant (plus grande facilité pour placer les diagnostics). On a, dans le cas cylindrique:

$$B = \frac{\mu}{2 \pi} \frac{I}{r} \quad P_{magn\acute{e}tiq... ...\Bigl( \frac{I}{r} \Bigr) }^2 \cdot {10}^{-5} \, \mbox{bars}$$

Dans le cas d'une charge carrée, pour laquelle $\alpha$ est la fraction du courant d'une face qui passe sur l'échantillon et $w$ est le diamètre de l'échantillon:

$$B = \mu \frac{I_{\acute{e}chantillon}}{w} \quad I_{\acute{e... ...\frac{I_{total}}{w} \Bigr) }^2 \cdot {10}^{-5} \, \mbox{bars}$$

La compression de flux permet donc de créer des formes temporelles de pressions variées. Il est donc possible de créer des chocs dans des échantillons ou bien d'autres formes de contraintes. Une forme optimale de pression consiste en une montée lente, puis de plus en plus rapide de la pression. Cette forme idéale permet la compression isentropique^3.3 d'un matériau. En fonction du matériau à étudier, il est important de pouvoir agir sur le niveau de pression maximum généré ainsi que sur le temps de montée et sur la concavité de la courbe temporelle de pression. On agit sur le temps de montée de la pression via la masse du liner réalisant la compression de flux, sur la concavité de la courbe via la forme (en général, simplement l'angle du cône) du barreau central et sur le pied de la courbe via le niveau de courant secondaire injecté (qui joue aussi sur la pression maximum atteignable, de concert avec le niveau de courant du primaire). Bien sur, ces tirs n'utilisent pas de pinch en tant que charge, mais seulement une inductance morte dans laquelle on injecte le courant issu de l'étage d'amplification de flux.

Notes

... magnétique^3.2

On peut utiliser $\delta \approx 25 \sqrt{\rho t}$ avec $t$ en $ns$, $\rho$ en $\Omega \cdot m$ et $\delta$ en $mm$ ou bien les courbes universelles données en section E.4 page

...compression!isentropique^3.3

C'est à dire une contrainte qui s'applique sans choc, donc de façon adiabatique et sans échauffement `` parasite ''.