H.1.8 Limitation du pas de temps
Afin de simuler la dynamique d'un phénomène physique de la façon la plus économe en temps de calcul, il convient d'utiliser
le pas de temps le plus grand possible. Toutefois, certaines valeurs limites existent, afin de garantir un calcul de
qualité ayant un sens physique. Ainsi, si un certain phénomène se propage à la vitesse  , dans des cellules de longueur
, dans des cellules de longueur
 dans le sens de la propagation, il faut s'assurer que l'on effectue plusieurs pas de calculs avant que le phénomène
n'ait traversé la cellule, et ceci impose que le pas de temps soit suffisamment faibleH.10
(pour plus de précisions, voir [78]).
Les phénomènes importants pour la MHD
peuvent être des ondes hydrodynamiques de vitesse
dans le sens de la propagation, il faut s'assurer que l'on effectue plusieurs pas de calculs avant que le phénomène
n'ait traversé la cellule, et ceci impose que le pas de temps soit suffisamment faibleH.10
(pour plus de précisions, voir [78]).
Les phénomènes importants pour la MHD
peuvent être des ondes hydrodynamiques de vitesse  et des ondes
d'Alfvén de vitesse
et des ondes
d'Alfvén de vitesse  .
Nous devons alors utiliser lors du calcul un pas de temps
.
Nous devons alors utiliser lors du calcul un pas de temps 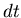 qui soit inférieur à :
qui soit inférieur à :
Notes
- ... faibleH.10
- En effet, si l'on imagine que le pas de
temps du calcul
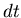 soit très grand devant le temps de traversée de la cellule par le phénomène considéré, alors on ne pourra de
toute façon pas propager ce dernier en un temps plus bref que
soit très grand devant le temps de traversée de la cellule par le phénomène considéré, alors on ne pourra de
toute façon pas propager ce dernier en un temps plus bref que 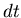 . Ceci signifie alors que la vitesse de propagation
simulée est fausse et sans aucun rapport avec la physique du phénomène.
. Ceci signifie alors que la vitesse de propagation
simulée est fausse et sans aucun rapport avec la physique du phénomène.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
