suivant: F.1.3.2 Piston magnétique monter: F.1.3 Considérations de pression précédent: F.1.3 Considérations de pression Table des matières Index
Le passage du courant produit de l'échauffement par effet Joule, ce qui tend à augmenter la pression thermique. Mais la diffusivité augmente avec la température pour un plasma proche de la température de fusion et à la densité voisine de celle du solide (minimum de conductivité pour un matériau atteinte juste à la mise en plasma). Ceci se voit d'ailleur, amplifié par la variation de densité, sur la courbe de diffusivité F.6. La pression magnétique a alors plus de mal à contenir la matière chaude, qui s'étend plus facilementF.7.
Si la pression thermique devient supérieure à la pression magnétique, alors le matériau s'étend, jusqu'à obtenir l'équilibre des pressions. Si la pression magnétique est supérieure à la pression thermique, alors la matière se fait compresser jusqu'à ce que sa pression interne équilibre la pression magnétique.
Enfin, il n'y a pas de contribution significative à la pression par un `` effet fusée '': les masses éjectées sont faibles, et surtout les vitesses sont faibles (toujours du fait du nombre de Reynolds magnétique).
Les deux pressions sont alors du même ordre de grandeur, là ou le courant circule.
Leur équilibre est perturbé d'une part par le nombre de Reynolds magnétique,
qui permet en étant voisin de ![]() à la matière de ne pas être parfaitement collée au
champ magnétique, et d'autre part au chauffage par onde de choc: sur la courbe
F.6 on voit nettement apparaitre entre
à la matière de ne pas être parfaitement collée au
champ magnétique, et d'autre part au chauffage par onde de choc: sur la courbe
F.6 on voit nettement apparaitre entre ![]() et
et
![]() un
plateau sur le profil de température, qui représente l'épaisseur dans laquelle
l'onde de choc s'est propagéeF.8. Le
matériau est donc préchauffé par rapport à la
partie plus interne de l'échantillon, qui n'était pas assez épaisse pour former un
choc.
un
plateau sur le profil de température, qui représente l'épaisseur dans laquelle
l'onde de choc s'est propagéeF.8. Le
matériau est donc préchauffé par rapport à la
partie plus interne de l'échantillon, qui n'était pas assez épaisse pour former un
choc.
Cet équilibre des pressions se traduit aussi par une équivalence (même ordre de
grandeur) des vitesses sonores et d'ALFVÉN: la pression magnétique est
égale à
![]() .
Or La vitesse d'Alfvén s'écrit
.
Or La vitesse d'Alfvén s'écrit
![]() ,
donc
,
donc
![]() . De la même façon, la
vitesse sonore
. De la même façon, la
vitesse sonore ![]() s'écrit en fonction de la pression
hydrodynamique
s'écrit en fonction de la pression
hydrodynamique
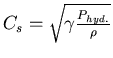 .
On en déduit donc que lorsque la pression magnétique et la
pression hydrodynamique sont égales, la vitesse
d'ALFVÉN est voisine de la vitesse sonore (en effet,
pour un gaz parfait,
.
On en déduit donc que lorsque la pression magnétique et la
pression hydrodynamique sont égales, la vitesse
d'ALFVÉN est voisine de la vitesse sonore (en effet,
pour un gaz parfait,
![]() ).
).