C.5.1 Plasma cinétique, plasma corrélé

Le comportement du plasma sera différent selon que les effets d'interactions entre particules dominent ou pas. On exprime ceci avec le paramètre de couplage $\Gamma$ :

$$\Gamma = \frac{E_{interaction}}{E_{cin\acute{e}tique}}$$

Si l'on considère que les particules ont 3 degrés de liberté, qu'elles sont toutes de même charge 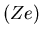$(Z e)$ et séparées d'une distance inter-particulaire moyenne $d$ exprimable simplement à partir du nombre de particules par unité de volume^C.35 $n$, et enfin que la seule force d'interaction est l'interaction électrique coulombienne :

$$\begin{eqnarray*} E_{cin\acute{e}tique} & = & \frac{3}{2}kT \\ E_{interacti... ...4 \pi \varepsilon d} \\ d & \approx & \frac{1}{\sqrt[3]{n}} \end{eqnarray*}$$

Alors on a :

$$\Gamma = \frac{{(Z e)}^2}{4 \pi \varepsilon} \cdot \frac{\sqrt[3]{n}}{\frac{3}{2}kT}$$ (C.34)

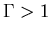Si $\Gamma$ est plus petit que $1$, alors le plasma est cinétique, c'est à dire dominé par les effets cinétiques des particules le composant. Dans le cas contraire ($\Gamma > 1$), alors le plasma est corrélé.

Notes

... volume^C.35

Ce nombre de particules par unité de volume se calcule en fonction de la densité $\rho$, du nombre d'Avogadro 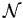$\mathcal{N}$ et de la masse atomique 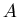$A$ (donnée en 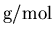$\mathrm{g/mol}$ dans les formulaires) : 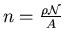$n = \frac{\rho \mathcal{N}}{A}$. Il est aussi possible de le calculer en se basant sur une boule: $d=\frac{1}{\sqrt[3]{\frac{4}{3} \pi n}}$. Cette distance est appellée rayon de Wigner-Seitz.