C.4.12 Nombre de REYNOLDS magnétique
Si l'on s'intéresse à l'équation (C.7) en négligeant le modèle de fluide électronique, il est possible de faire
apparaître deux termes décrivant deux effets :
-
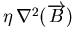
- qui décrit la diffusion du champ magnétique dans un milieu ayant une
diffusivité
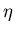 ;
;
-
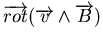
- qui décrit l'entraînement du champ magnétique par le fluide en
mouvement.
Une façon de quantifier l'équilibre entre ces deux phénomènes consiste à comparer leurs effets respectifs, via leur vitesse
d'évolution caractéristique :
-
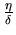 pour la diffusion résistive
(
pour la diffusion résistive
(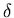 étant l'épaisseur de peau
magnétique) ;
étant l'épaisseur de peau
magnétique) ;
 pour le déplacement du plasma.
pour le déplacement du plasma.
Le nombre de Reynolds magnétique se définit alors comme :
 |
(C.30) |
Dans le cas 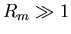 , l'effet d'entraînement est dominant.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
, l'effet d'entraînement est dominant.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
