C.3.1 Équation de la continuité hydrodynamique

**Figure:** équation de la continuité hydrodynamique
$\rotatebox{-90}{\includegraphics[height=0.3\textwidth]{figures/eqcont.ps}}$

On appelle débit du fluide le flux de masse à travers une surface : 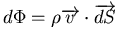$d\Phi = \rho \overrightarrow{v} \cdot \overrightarrow{dS}$ , les surfaces étant orientées vers l'extèrieur. La conservation de la quantité de matière pour un élément de volume

de surface

s'écrit alors :

$\begin{displaymath} \frac{d}{dt} \int \!\!\!\! \int \!\!\!\! \int_V \rho \, dV... ...!\! \int_S \rho \overrightarrow{v} \cdot \overrightarrow{dS} \end{displaymath}$

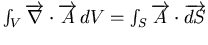Or $\int_V \overrightarrow{\nabla} \cdot \overrightarrow{A} \, dV = \int_S \overrightarrow{A} \cdot \overrightarrow{dS}$ , et si l'on considère que le volume

ne varie pas au cours du temps^C.11, alors on a :

$\begin{displaymath} \frac{d \, \rho}{dt} + \mathop{div}(\rho \overrightarrow{v}) = 0 \end{displaymath}$

(C.9)

Ceci signifiant que la variation de matière dans un volume donné est uniquement produite par de la matière qui entre ou qui sort de ce volume.

Notes

... temps ^C.11: Afin que $\frac{d}{dt}$ puisse passer sous le signe somme

Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002