I.3.1 Calcul des facteurs de pertes
Afin de calculer ces facteurs, il est possible d'utiliser deux paramètres issus du recalage avec l'expérience :
- la puissance rayonnée maximum;
- le temps auquel on atteint ce maximum.
Bien sur, le même raisonnement peut être transposé au courant secondaire maximum. Il faut avant toutes choses disposer d'une
simulation de l'expérience servant de référence dans laquelle les coefficients sont choisis arbitrairement.
Nous allons alors chercher quels sont les facteurs multiplicatifs à appliquer aux courants précédemment injectés dans la
simulation pour faire coïncider nos deux paramètres de recalage entre la simulation et l'expérience. Pour cela,
on utilise l'approximation

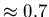 ;
;
-
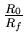
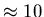 en général;
en général;

- est la hauteur du pinch;

- est le courant maximum appliqué au pinch (donc ici,
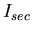 maximum).
maximum).
d'où
De même, on peut faire l'approximation
On en déduit
Il suffit alors de calibrer le coefficient 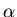 avec des résultats expérimentaux fiablesI.3.
avec des résultats expérimentaux fiablesI.3.
On considère alors que le taux de compression reste constant, donc que le facteur multiplicatif à appliquer sur le courant
secondaire maximum s'applique aussi sur le courant secondaire au moment du crowbar. Le facteur de pertes du
générateur secondaire est donc fixé.
En utilisant le paramètre
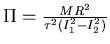 caractéristique de la dynamique du liner dans le
cas de la compression de flux, et en faisant l'approximation que les formes des courants au cours du temps restent
identiques malgré une dynamique un petit peu différente, on obtient :
caractéristique de la dynamique du liner dans le
cas de la compression de flux, et en faisant l'approximation que les formes des courants au cours du temps restent
identiques malgré une dynamique un petit peu différente, on obtient :
Avec  représentant l'intervalle de temps entre le temps du maximum du courant secondaire et le temps du crowbar.
Donc en connaissant les valeurs maximum des courants primaires et secondaire (après amplification) lors de la simulation
initiale, il est possible de calculer le facteur à appliquer au courant primaire.
représentant l'intervalle de temps entre le temps du maximum du courant secondaire et le temps du crowbar.
Donc en connaissant les valeurs maximum des courants primaires et secondaire (après amplification) lors de la simulation
initiale, il est possible de calculer le facteur à appliquer au courant primaire.
Notes
- ... fiablesI.3
- en utilisant l'énergie
rayonnée pour calculer une vitesse, et en utilisant cette vitesse et la puissance rayonnée pour calculer le coefficient de
proportionnalité
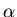 .
.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
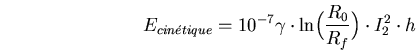
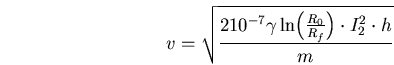
![\begin{displaymath}
I_2 = \sqrt[3]{\frac{P_{rayonn\acute{e}e}}{\alpha \cdot m}}...
... {10}^{-7} \gamma \ln \Bigl( \frac{R_0}{R_f} \Bigr) \cdot h}}
\end{displaymath}](img1569.png)
![]() caractéristique de la dynamique du liner dans le
cas de la compression de flux, et en faisant l'approximation que les formes des courants au cours du temps restent
identiques malgré une dynamique un petit peu différente, on obtient :
caractéristique de la dynamique du liner dans le
cas de la compression de flux, et en faisant l'approximation que les formes des courants au cours du temps restent
identiques malgré une dynamique un petit peu différente, on obtient :