D.6.2 Résistivité anormale

Lors d'une simulation numérique mettant en jeu le passage de courant dans un plasma, le problème de la limitation du courant dans les basses densité se pose. En effet, si le maillage est suffisamment fin pour permettre à des cellules de contenir des densités très faibles et que celles-ci sont exposées à la source de courant, alors le chauffage ohmique conduit à une très forte augmentation de température, donc la conductivité de ces cellules augmente fortement, et celles-ci détournent encore plus de courant ...

Ce problème pourrait provenir de deux causes:

• un modèle de résistivité trop grossier, qui évaluerait mal certains effets ;
• un manque dans les équations résolues par les codes MHD utilisés ;
• L'absence de prise en compte de certains phénomènes physiques se produisant lors de fortes densités de courant.

La première explication signifierait qu'il faudrait reprendre dans le détail les modèles actuels pour en éliminer toute approximation abusive. C'est le type de travail réalisé par DESJARLAIS (c'est en tout cas l'un des objectifs, d'après [32])

La seconde possibilité peut être liée à la loi d'Ohm et à l'équation de l'énergie. Ainsi, les termes d'effets NERNST (en $\overrightarrow{B} \wedge \mathop{\overrightarrow{grad}}({T})$ dans la loi d'ohm) et ETTINGHAUSEN (en $\overrightarrow{B} \wedge \overrightarrow{j}$ sur l'énergie) permettent de limiter le courant de façon très satisfaisante en 1D (voir [20]). En 2D , l'ajout des termes d'effets HALL (en $\overrightarrow{B} \wedge \overrightarrow{j}$ dans la loi d'ohm) et LEDUC-RIGHI (en $\overrightarrow{B} \wedge \mathop{\overrightarrow{grad}}({T})$ sur l'énergie) devraient pouvoir jouer un rôle de limitation du courant (d'après [18]).

Tableau: classification des effets thermoélectriques

forme	loi d'ohm	équation de l'énergie
$\overrightarrow{B} \wedge \mathop{\overrightarrow{grad}}({T})$	Nernst	Leduc-Righi
	en 1D	en 2D
$\overrightarrow{B} \wedge \overrightarrow{j}$	Hall	Ettinghausen
	en 2D	en 1D

Enfin, la dernière possibilité introduit la notion de résistivité anormale. Ceci signifierait que de nouveaux phénomènes physiques se produiraient lors du passage d'un courant intense dans des densités faibles. Un modèle simple et qui semble donner de bons résultats est l'instabilité hybride basse. Les micro-instabilités apparaissent lorsque la vitesse de dérive $v_D$ des électrons dépasse la vitesse locale du son $C_s$. La micro-instabilité ayant le taux de croissance le plus important pour un pinch est l'instabilité hybride basse. Celle-ci est créée par les gradients de courant (il s'agit d'une instabilité électronique), de densité et de température.

Le temps caractéristique de croissance est de l'ordre de l'inverse de la fréquence hybride basse

$$\omega_{LH}^2 \approx \frac{\Omega_p^2}{1+\frac{\omega_p^2}{\omega_c^2}}$$

Les grandeurs en $\Omega$ sont liées aux ions, celles en $\omega$ aux électrons. Les grandeurs indicées en $X_p$ désignent des fréquences plasma et celles en $X_c$ des fréquences cyclotron. En pratique, pour un pinch, le temps de croissance est très faible devant le temps d'évolution macroscopique du plasma. La longueur caratéristique de cette instabilité est de l'ordre du libre parcour moyen électronique.

La fréquence de collision retenue est alors la somme entre la fréquence de collision normale ($\nu_{ei}$ par exemple) et une fréquence de collision anormale $\nu_{anom.}$ telle que

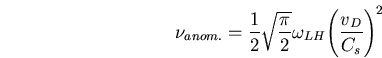$$\nu_{anom.} = \frac{1}{2} \sqrt{\frac{\pi}{2}} \omega_{LH} {\Biggl( \frac{v_D}{C_s} \Biggr)}^2$$ (D.16)

Il faut tout de même garder à l'esprit que ce modèle n'a pas encore été étudié dans le cas d'un pinch (voir [17]), et que cette interprétation ne fait pas forcément l'unanimité.