1.3.1.1 Optimisations géométriques

Le flux piégé au moment du crowbar est donc:

$$\Phi_0 = L_0 I_0 = \Biggl( \frac{\mu_0}{2 \pi} H \ln \Bigl... ...2 \pi} h \ln \Bigl( \frac{r}{r_b} \Bigr) \Biggr) \cdot I_0$$

A un moment quelconque de l'implosion, le flux piégé est, en supposant une stricte conservation du flux:

$$\Phi = L I = \Biggl( \frac{\mu_0}{2 \pi} H \ln \Bigl( \fra... ...}{2 \pi} h \ln \Bigl( \frac{r}{r_b} \Bigr) \Biggr) \cdot I$$

D'après la conservation du flux, on obtient:

$$\begin{eqnarray*} \frac{I}{I_0} & = & \frac{\ln \frac{R_0}{r_b} + \frac{h}{H} ... ...& \frac{H}{h} \frac{\ln \frac{R_0}{r_b}}{\ln \frac{r}{r_b}} +1 \end{eqnarray*}$$

De façon à optimiser la compression (c'est à dire à maximiser 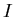$I$), il faut:

• $H \gg h$
• $R_0 \gg r_b$
• $r \approx r_b$

Dans le cas où le liner ne s'arrete pas à $R=r_b$, mais un petit peu avant, l'optimisation est moins bonne. Si l'on note $R_f$ le rayon atteint par le liner en fin de compression (c'est à dire le rayon minimal), il faut:

• $R_f \approx r_b$