suivant: E.3.2.3 Calcul de l'épaisseur monter: E.3.2 Méthode utilisée précédent: E.3.2.1 Limitation de la Table des matières Index
de l'espace et à un temps 
, la première contribution est issue d'une formule analytique (en
effet,
est simplifiable et évite ainsi une forme indéterminée
qui numériquement aurait produit des instabilités). Le premier pas d'échantillonnage
en 
est imposé à
où
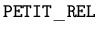représente un nombre
petit. Ceci permet de se fixer un pas d'échantillonnage initial caractéristique de
l'échelle du problème. Ensuite, les contributions successives sont ajoutées, à la
condition que ces contributions soient suffisamment faibles par rapport à la somme
partielle en cours de calcul. Dans le cas contraire, le pas d'échantillonnage est
divisé par deux et le calcul recommence (si ces contributions sont au contraire trop
faibles, le pas est multiplié par deux). Afin de conserver un temps de calcul
raisonnable, le pas de temps ne peut descendre en dessous d'une valeur minimum.
L'ajout à la somme partielle est ensuite fait, via une intégration par la méthode des
trapèzes. La somme est considérée comme ayant convergée lorsque ces ajouts sont
suffisamment faibles devant la somme calculée.