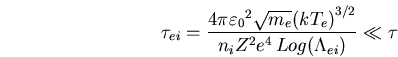C.5.6 Modèle à une température, modèle à deux températures
Une description à une température d'un plasma peut être suffisante si les temps caractéristiques d'échange de l'énergie
entre les ions et les électrons sont courts devant le temps caractéristique d'évolution du système. Dans un tel cas, alors
les températures s'égalisent sans que le système n'ait évolué. Ces temps caractéristiques sont en fait liés à la fréquence
de collision électrons/ions. Si  est un temps caractéristique d'évolution du système, alors un modèle à une
température est suffisant si
est un temps caractéristique d'évolution du système, alors un modèle à une
température est suffisant si
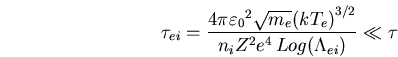 |
(C.39) |
Dans le cas d'un Z-pinch, un temps caractéristique du système est lié au
chauffage Joule, ce qui s'exprime
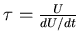 avec
avec
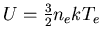 et
et
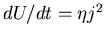 (voir [20]).
(voir [20]).
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002