1.2.1 Démonstration de la conservation du flux
Figure:
conservation du flux magnétique
|
|
Soit  un contour parfaitement conducteur et
un contour parfaitement conducteur et  une surface s'appuyant sur ce contour. Dans cette
surface, il existe un flux magnétique
une surface s'appuyant sur ce contour. Dans cette
surface, il existe un flux magnétique  créé par la présence d'un champ magnétique
créé par la présence d'un champ magnétique
 tel que
tel que
Ceci signifie que
D'où:
Ensuite, d'après les équations de Maxwell, on a
 , et d'après les propriétés du rotationnel:
, et d'après les propriétés du rotationnel:
Puisque  est un contour conducteur idéal, alors
est un contour conducteur idéal, alors
 ; ceci permet
d'établir que
; ceci permet
d'établir que
Enfin, cela signifie que
dans la surface  s'appuyant sur un contour
s'appuyant sur un contour  conducteur idéal. Le flux magnétique est donc conservé
dans une surface délimitée par un conducteur.
conducteur idéal. Le flux magnétique est donc conservé
dans une surface délimitée par un conducteur.
Mathias.Bavay_at_ingenieurs-supelec.org - juillet 2002
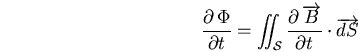
 , et d'après les propriétés du rotationnel:
, et d'après les propriétés du rotationnel:
